《2025年亮点给力提优课时作业本九年级物理上册苏科版》

13. 某工地的施工现场,一台起重机的钢丝绳正吊着一箱重物匀速竖直上升,下列图示的图像中,能正确反映钢丝绳的拉力所做的功 W 与时间 t 关系的是 ()

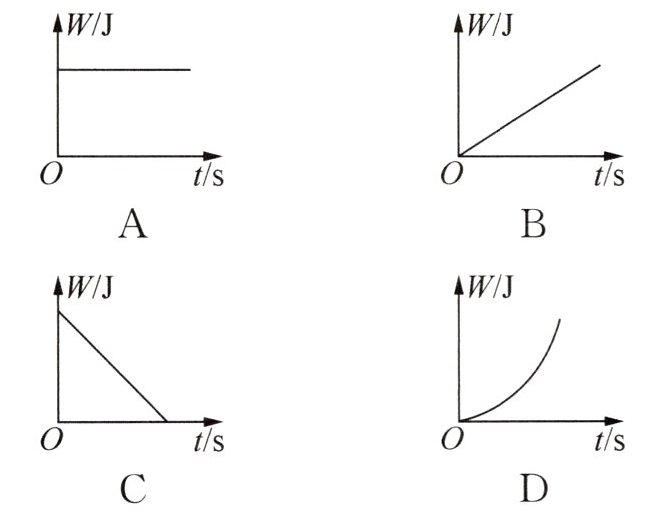
答案： B

14. 新趋势 学科融合 我们计算做功的时候,除了应用公式来求解功外,还可以画出物体受力 F 与在力的方向移动的距离 s 的图像,如图甲所示,用图像下方的面积来表示力 F 做的功,若力与距离的关系满足$F = ks或F = ks + b(k ≠ 0)$,则图像下方的三角形或梯形面积都可以作为做功的值. 用铁锤把小钉钉入木板(如图乙所示),设木板对小钉的阻力与钉进的深度成正比,已知铁锤第一次对钉子做功为 W,将钉子钉进的深度为 d,如果第二次敲钉子时将钉子钉进的深度又为 d,则第二次做功为______(用题目中所给物理量符号表示).

答案：
3W 解析：由题意可知，木板对小钉的阻力 $ f $ 与钉进的深度 $ s $ 成正比，设其 $ f - s $ 图像如图所示，设 $ f = ks $，则 $ f_1 = kd $、$ f_2 = kd' $，如果第二次敲钉子时将钉子钉进的深度又为 $ d $，即 $ d' = 2d $，则 $ f_2 = k \times 2d = 2kd = 2f_1 $。根据题中所述用图像面积求功的方法，铁锤第一次对钉子做功 $ W = \frac{1}{2}f_1d $，第二次做功 $ W' = \frac{1}{2}f_2d' - W = \frac{1}{2} \times 2f_1 \times 2d - W = 4W - W = 3W $。

15. 新素养 科学思维 一根质量分布不均匀的金属棒 AB 置于水平地面上,小明用弹簧测力计竖直地将棒的 B 端缓慢拉起,如图甲所示,在此过程中,弹簧测力计对棒所做的功 W 与 B 端离开地面的高度 x 的关系如图乙所示,其中 OP 段为 A 端离开地面前,PQ 段为 A 端离开地面后.

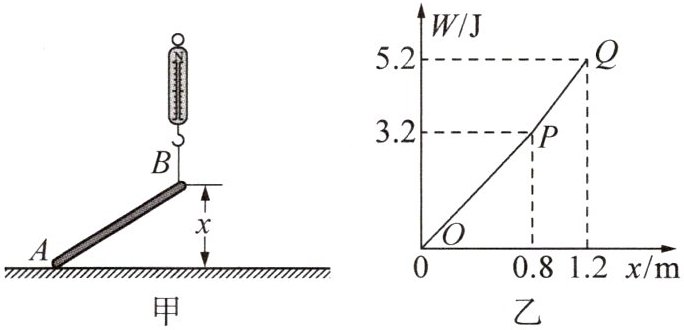
(1) 金属棒的长度为______m.
(2) 金属棒的重力为______N.
(3) 小明用同样的方式使用弹簧测力计竖直将棒的 A 端拉起,A 端刚好被拉起时测力计的示数为______N.

答案：
(1) 0.8
(2) 5
(3) 1 解析：
(1) 由图乙可知，当 $ B $ 端离地 0.8 m 时，$ A $ 端刚离地，所以金属棒长度为 0.8 m。
(2) 因为 $ W = Gh $，所以金属棒的重力 $ G = \frac{\Delta W}{\Delta h} = \frac{5.2 \, \text{J} - 3.2 \, \text{J}}{1.2 \, \text{m} - 0.8 \, \text{m}} = 5 \, \text{N} $。
(3) 由于拉力始终竖直向上，重力的方向竖直向下，动力臂与阻力臂之比不变，由杠杆的平衡条件可知，金属棒未离地时的拉力大小不变。由图乙可知，金属棒未离地时测力计的拉力 $ F_1 = \frac{W}{h} = \frac{3.2 \, \text{J}}{0.8 \, \text{m}} = 4 \, \text{N} $。由杠杆的平衡条件可得 $ F_1l_{AB} = Gd $，则重心到 $ A $ 端的距离 $ d = \frac{F_1l_{AB}}{G} = \frac{4 \, \text{N} \times 0.8 \, \text{m}}{5 \, \text{N}} = 0.64 \, \text{m} $；当用同样的方式使用弹簧测力计竖直将棒的 $ A $ 端拉起，同理可得 $ F_2l_{AB} = G(l_{AB} - d) $，则 $ F_2 = \frac{G(l_{AB} - d)}{l_{AB}} = \frac{5 \, \text{N} \times (0.8 \, \text{m} - 0.64 \, \text{m})}{0.8 \, \text{m}} = 1 \, \text{N} $，即 $ A $ 端刚好被拉起时弹簧测力计的示数为 1 N。