第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
7. [2025 安徽阜阳太和期末]如图,$P是边长为2的正方形ABCD$内的一个

动点,且满足$\angle PDC= \angle PCB$,则$AP$的最小值是( )
A. $4-\sqrt{5}$
B. $1$
C. $\sqrt{5}$
D. $\sqrt{5}-1$

动点,且满足$\angle PDC= \angle PCB$,则$AP$的最小值是( )
A. $4-\sqrt{5}$
B. $1$
C. $\sqrt{5}$
D. $\sqrt{5}-1$
答案:
D
∵ 四边形 $ABCD$ 是正方形,
∴ $∠BCD = 90^{\circ}$,
∵ $∠PDC = ∠PCB$,
∴ $∠PDC + ∠PCD = 90^{\circ}$,
∴ $∠DPC = 90^{\circ}$,
∴ 点 $P$ 在以 $CD$ 为直径的圆上,
如图,取 $CD$ 的中点 $M$,连接 $AM$,$PM$,则 $M$ 是该圆的圆心,点 $A$ 在 $⊙M$ 外,$CM = DM = 1$,
在 $△APM$ 中,$AP > AM - PM$,
∴ 当 $A$,$P$,$M$ 三点共线时,$AP$ 有最小值,此时 $AP = AM - PM = \sqrt{1^{2} + 2^{2}} - 1 = \sqrt{5} - 1$。故选 D。

D
∵ 四边形 $ABCD$ 是正方形,
∴ $∠BCD = 90^{\circ}$,
∵ $∠PDC = ∠PCB$,
∴ $∠PDC + ∠PCD = 90^{\circ}$,
∴ $∠DPC = 90^{\circ}$,
∴ 点 $P$ 在以 $CD$ 为直径的圆上,
如图,取 $CD$ 的中点 $M$,连接 $AM$,$PM$,则 $M$ 是该圆的圆心,点 $A$ 在 $⊙M$ 外,$CM = DM = 1$,
在 $△APM$ 中,$AP > AM - PM$,
∴ 当 $A$,$P$,$M$ 三点共线时,$AP$ 有最小值,此时 $AP = AM - PM = \sqrt{1^{2} + 2^{2}} - 1 = \sqrt{5} - 1$。故选 D。

8. [2025 北京西城期中]如图,以点$G(0,1)$为圆心,$2为半径的圆与x轴交于A$,$B$两点,与$y轴交于C$,$D$两点,$E为\odot G$上一动点,$CF\perp AE于点F$,连接$FG$,则弦$AB$的长度为______;点$E在\odot G$上运动的过程中,线段$FG$的长度的最小值为______。
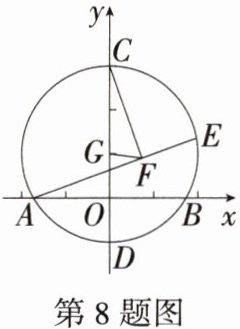

答案:
答案 $2\sqrt{3}$;$\sqrt{3} - 1$
解析 如图,连接 $AG$。
∵ $GO⊥AB$,
∴ $OA = OB$,在 $Rt△AGO$ 中,
∵ $AG = 2$,$OG = 1$,
∴ $AG = 2OG$,$OA = \sqrt{2^{2} - 1^{2}} = \sqrt{3}$,
∴ $∠GAO = 30^{\circ}$,$AB = 2AO = 2\sqrt{3}$。
连接 $AC$,
∵ $OA = \sqrt{3}$,$OC = 3$,
∴ $AC = 2\sqrt{3}$。
∵ $CF⊥AE$,
∴ 点 $F$ 在以 $AC$ 为直径的圆上,
取 $AC$ 的中点 $M$,连接 $MF$,$MG$,则有 $FG≥FM - GM$,
∵ $GA = GC$,$MA = MC$,
∴ $GM$ 垂直平分 $AC$,
∵ $GC = GA$,
∴ $∠GCA = ∠GAC = 30^{\circ}$,
∴ $MG = \frac{1}{2}AG = 1$,
∵ $M$ 为 $AC$ 中点,$∠CFA = 90^{\circ}$,
∴ $FM = \frac{1}{2}AC = \sqrt{3}$,
∴ $FG$ 的最小值为 $FM - GM = \sqrt{3} - 1$。

答案 $2\sqrt{3}$;$\sqrt{3} - 1$
解析 如图,连接 $AG$。
∵ $GO⊥AB$,
∴ $OA = OB$,在 $Rt△AGO$ 中,
∵ $AG = 2$,$OG = 1$,
∴ $AG = 2OG$,$OA = \sqrt{2^{2} - 1^{2}} = \sqrt{3}$,
∴ $∠GAO = 30^{\circ}$,$AB = 2AO = 2\sqrt{3}$。
连接 $AC$,
∵ $OA = \sqrt{3}$,$OC = 3$,
∴ $AC = 2\sqrt{3}$。
∵ $CF⊥AE$,
∴ 点 $F$ 在以 $AC$ 为直径的圆上,
取 $AC$ 的中点 $M$,连接 $MF$,$MG$,则有 $FG≥FM - GM$,
∵ $GA = GC$,$MA = MC$,
∴ $GM$ 垂直平分 $AC$,
∵ $GC = GA$,
∴ $∠GCA = ∠GAC = 30^{\circ}$,
∴ $MG = \frac{1}{2}AG = 1$,
∵ $M$ 为 $AC$ 中点,$∠CFA = 90^{\circ}$,
∴ $FM = \frac{1}{2}AC = \sqrt{3}$,
∴ $FG$ 的最小值为 $FM - GM = \sqrt{3} - 1$。

9. [2024 江苏南京建邺月考]如图,在矩形$ABCD$中,$AB= 6$,$AD= 8$,$P$是矩形内部的一个动点,且$\angle APD= 90^{\circ}$,连接$CP并延长交AB于E$,则$AE$的最大值为______。


答案:
答案 $\frac{8}{3}$
解析
∵ $∠APD = 90^{\circ}$,
∴ 点 $P$ 在以线段 $AD$ 的中点 $O$ 为圆心,$AD$ 为直径的圆上,易知当 $EC$ 与圆 $O$ 相切时,$AE$ 的值最大。如图,设 $CE$ 与圆 $O$ 相切于点 $F$,由切线长定理得 $AE = EF$,$CF = CD = 6$,在 $Rt△BCE$ 中,$BE = 6 - AE$,$EC = EF + FC = 6 + AE$,$BC = 8$,由勾股定理得 $(6 - AE)^{2} + 8^{2} = (6 + AE)^{2}$,
∴ $AE = \frac{8}{3}$。即 $AE$ 的最大值为 $\frac{8}{3}$。
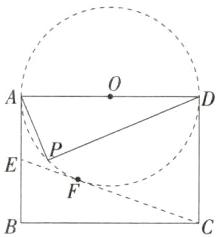
答案 $\frac{8}{3}$
解析
∵ $∠APD = 90^{\circ}$,
∴ 点 $P$ 在以线段 $AD$ 的中点 $O$ 为圆心,$AD$ 为直径的圆上,易知当 $EC$ 与圆 $O$ 相切时,$AE$ 的值最大。如图,设 $CE$ 与圆 $O$ 相切于点 $F$,由切线长定理得 $AE = EF$,$CF = CD = 6$,在 $Rt△BCE$ 中,$BE = 6 - AE$,$EC = EF + FC = 6 + AE$,$BC = 8$,由勾股定理得 $(6 - AE)^{2} + 8^{2} = (6 + AE)^{2}$,
∴ $AE = \frac{8}{3}$。即 $AE$ 的最大值为 $\frac{8}{3}$。

10. [2024 山东淄博桓台二模]如图,在$\triangle ABC$中,$\angle BAC= 60^{\circ}$,$AD\perp BC于点D$,且$AD= 4$,则$\triangle ABC$面积的最小值为______。


答案:
答案 $\frac{16\sqrt{3}}{3}$
解析 如图,作 $△ABC$ 的外接圆 $⊙O$,连接 $OA$,$OB$,$OC$,过点 $O$ 作 $OE⊥BC$ 于点 $E$,
∵ $∠BAC = 60^{\circ}$,
∴ $∠BOC = 120^{\circ}$,
∵ $OB = OC$,
∴ $∠OBC = ∠OCB = 30^{\circ}$,设 $⊙O$ 的半径为 $r$,则 $OE = \frac{1}{2}OB = \frac{1}{2}r$,$BE = \frac{\sqrt{3}}{2}OB = \frac{\sqrt{3}}{2}r$,
∴ $BC = \sqrt{3}r$,
∵ $OA + OE≥AD$,
∴ $r + \frac{1}{2}r≥4$,解得 $r≥\frac{8}{3}$,
∴ $BC≥\frac{8\sqrt{3}}{3}$,
∴ $S_{△ABC} = \frac{1}{2}BC·AD≥\frac{1}{2}×\frac{8\sqrt{3}}{3}×4 = \frac{16\sqrt{3}}{3}$,
∴ $△ABC$ 面积的最小值为 $\frac{16\sqrt{3}}{3}$。

答案 $\frac{16\sqrt{3}}{3}$
解析 如图,作 $△ABC$ 的外接圆 $⊙O$,连接 $OA$,$OB$,$OC$,过点 $O$ 作 $OE⊥BC$ 于点 $E$,
∵ $∠BAC = 60^{\circ}$,
∴ $∠BOC = 120^{\circ}$,
∵ $OB = OC$,
∴ $∠OBC = ∠OCB = 30^{\circ}$,设 $⊙O$ 的半径为 $r$,则 $OE = \frac{1}{2}OB = \frac{1}{2}r$,$BE = \frac{\sqrt{3}}{2}OB = \frac{\sqrt{3}}{2}r$,
∴ $BC = \sqrt{3}r$,
∵ $OA + OE≥AD$,
∴ $r + \frac{1}{2}r≥4$,解得 $r≥\frac{8}{3}$,
∴ $BC≥\frac{8\sqrt{3}}{3}$,
∴ $S_{△ABC} = \frac{1}{2}BC·AD≥\frac{1}{2}×\frac{8\sqrt{3}}{3}×4 = \frac{16\sqrt{3}}{3}$,
∴ $△ABC$ 面积的最小值为 $\frac{16\sqrt{3}}{3}$。

11. 如图,在$Rt\triangle ABC$中,$\angle ACB= 90^{\circ}$,$AC= BC= 1$,动点$M$、$N在斜边AB$上,$\angle MCN= 45^{\circ}$,则$MN$的最小值为______。


答案:
答案 $2 - \sqrt{2}$
解析 如图①,
∵ $∠MCN = 45^{\circ}$,
∴ 在 $AB$ 上方以 $MN$ 为斜边作等腰 $Rt△MON$,作 $△CMN$ 的外接圆 $⊙O$,连接 $OC$,取 $MN$ 的中点 $P$,$AB$ 的中点 $Q$,连接 $OP$、$CP$、$CQ$,设 $⊙O$ 的半径为 $r$,在 $Rt△ABC$ 中,$AC = BC = 1$,
∴ $AB = \sqrt{2}$,
∴ $CQ = \frac{\sqrt{2}}{2}$,在 $Rt△MON$ 中,$OM = ON = r$,
∴ $MN = \sqrt{2}r$,
∴ $OP = \frac{\sqrt{2}}{2}r$。
∵ $OC + OP≥CP≥CQ$,
∴ $r + \frac{\sqrt{2}}{2}r≥CP≥\frac{\sqrt{2}}{2}$。如图②,当且仅当点 $C$、$O$、$P$ 共线,且 $CP$ 与 $CQ$ 重合时,$r + \frac{\sqrt{2}}{2}r = \frac{\sqrt{2}}{2}$,此时 $r$ 最小,解得 $r = \sqrt{2} - 1$,
∴ $MN = \sqrt{2}r = 2 - \sqrt{2}$,即 $MN$ 的最小值为 $2 - \sqrt{2}$。


答案 $2 - \sqrt{2}$
解析 如图①,
∵ $∠MCN = 45^{\circ}$,
∴ 在 $AB$ 上方以 $MN$ 为斜边作等腰 $Rt△MON$,作 $△CMN$ 的外接圆 $⊙O$,连接 $OC$,取 $MN$ 的中点 $P$,$AB$ 的中点 $Q$,连接 $OP$、$CP$、$CQ$,设 $⊙O$ 的半径为 $r$,在 $Rt△ABC$ 中,$AC = BC = 1$,
∴ $AB = \sqrt{2}$,
∴ $CQ = \frac{\sqrt{2}}{2}$,在 $Rt△MON$ 中,$OM = ON = r$,
∴ $MN = \sqrt{2}r$,
∴ $OP = \frac{\sqrt{2}}{2}r$。
∵ $OC + OP≥CP≥CQ$,
∴ $r + \frac{\sqrt{2}}{2}r≥CP≥\frac{\sqrt{2}}{2}$。如图②,当且仅当点 $C$、$O$、$P$ 共线,且 $CP$ 与 $CQ$ 重合时,$r + \frac{\sqrt{2}}{2}r = \frac{\sqrt{2}}{2}$,此时 $r$ 最小,解得 $r = \sqrt{2} - 1$,
∴ $MN = \sqrt{2}r = 2 - \sqrt{2}$,即 $MN$ 的最小值为 $2 - \sqrt{2}$。


12. 如图,在四边形$ABCD$中,$AB= AD= CD= 4$,$AD// BC$,$\angle B= 60^{\circ}$,点$E$、$F分别为边BC$、$CD$上的动点,且$\angle EAF= 60^{\circ}$,则$\triangle AEF$面积的最小值是______。


答案:
答案 $4\sqrt{3}$
解析 如图,将 $△ADF$ 绕点 $A$ 顺时针旋转 $120^{\circ}$ 到 $△ABM$,由旋转得 $BM = DF$,$AM = AF$,$∠ABM = ∠D = 120^{\circ}$,$∠MAF = 120^{\circ}$,
∵ $∠ABC = 60^{\circ}$,
∴ $∠ABM + ∠ABC = 180^{\circ}$,
∴ $M$、$B$、$E$ 三点共线,
∵ $∠EAF = 60^{\circ}$,
∴ $∠MAE = 120^{\circ} - 60^{\circ} = 60^{\circ}$。又
∵ $AM = AF$,$AE = AE$,
∴ $△MAE≌△FAE(SAS)$,
∴ $∠MEA = ∠FEA$,过点 $A$ 作 $AH⊥BC$ 于 $H$,作 $AK⊥EF$ 于 $K$,
∴ $AH = AK = 2\sqrt{3}$,作 $△AEF$ 的外接圆 $⊙O$,连接 $OA$、$OE$、$OF$,过点 $O$ 作 $ON⊥EF$ 于 $N$,
∵ $∠EAF = 60^{\circ}$,
∴ $∠EOF = 120^{\circ}$,
∴ $∠NOF = 60^{\circ}$,设 $EF = 2x$,则 $NF = x$,在 $Rt△ONF$ 中,易得 $ON = \frac{\sqrt{3}}{3}x$,$OF = \frac{2\sqrt{3}}{3}x$,
∴ $ON + OA = ON + OF = \sqrt{3}x$,
∵ $OA + ON≥AK$,
∴ $\sqrt{3}x≥2\sqrt{3}$,
∴ $x≥2$,
∴ $S_{△AEF} = \frac{1}{2}EF·AK = \frac{1}{2}×2x×2\sqrt{3} = 2\sqrt{3}x≥4\sqrt{3}$,
∴ $△AEF$ 面积的最小值是 $4\sqrt{3}$。

答案 $4\sqrt{3}$
解析 如图,将 $△ADF$ 绕点 $A$ 顺时针旋转 $120^{\circ}$ 到 $△ABM$,由旋转得 $BM = DF$,$AM = AF$,$∠ABM = ∠D = 120^{\circ}$,$∠MAF = 120^{\circ}$,
∵ $∠ABC = 60^{\circ}$,
∴ $∠ABM + ∠ABC = 180^{\circ}$,
∴ $M$、$B$、$E$ 三点共线,
∵ $∠EAF = 60^{\circ}$,
∴ $∠MAE = 120^{\circ} - 60^{\circ} = 60^{\circ}$。又
∵ $AM = AF$,$AE = AE$,
∴ $△MAE≌△FAE(SAS)$,
∴ $∠MEA = ∠FEA$,过点 $A$ 作 $AH⊥BC$ 于 $H$,作 $AK⊥EF$ 于 $K$,
∴ $AH = AK = 2\sqrt{3}$,作 $△AEF$ 的外接圆 $⊙O$,连接 $OA$、$OE$、$OF$,过点 $O$ 作 $ON⊥EF$ 于 $N$,
∵ $∠EAF = 60^{\circ}$,
∴ $∠EOF = 120^{\circ}$,
∴ $∠NOF = 60^{\circ}$,设 $EF = 2x$,则 $NF = x$,在 $Rt△ONF$ 中,易得 $ON = \frac{\sqrt{3}}{3}x$,$OF = \frac{2\sqrt{3}}{3}x$,
∴ $ON + OA = ON + OF = \sqrt{3}x$,
∵ $OA + ON≥AK$,
∴ $\sqrt{3}x≥2\sqrt{3}$,
∴ $x≥2$,
∴ $S_{△AEF} = \frac{1}{2}EF·AK = \frac{1}{2}×2x×2\sqrt{3} = 2\sqrt{3}x≥4\sqrt{3}$,
∴ $△AEF$ 面积的最小值是 $4\sqrt{3}$。

查看更多完整答案,请扫码查看


