第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 下列命题正确的是(
A. 各边相等的多边形是正多边形
B. 正多边形一定是中心对称图形
C. 正多边形外接圆的圆心角是它的中心角
D. 正多边形外接圆的半径是它的半径
D
)A. 各边相等的多边形是正多边形
B. 正多边形一定是中心对称图形
C. 正多边形外接圆的圆心角是它的中心角
D. 正多边形外接圆的半径是它的半径
答案:
D 各边相等,各内角相等的多边形是正多边形,故 A 错误;当正多边形的边数为偶数时,它一定是中心对称图形,故 B 错误;正多边形每一边所对的圆心角是它的中心角,故 C 错误;正多边形外接圆的半径是正多边形的半径,故 D 正确。故选 D。
2. [2024 四川南充模拟]如图,A,B,C 是正多边形的顶点,O 是正多边形的中心,若△AOC 是等边三角形,则正多边形的边数为(
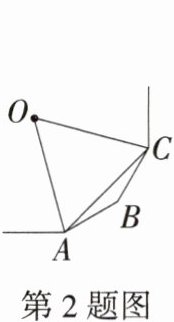
A. 6
B. 9
C. 12
D. 15
C
)
A. 6
B. 9
C. 12
D. 15
答案:
C 连接 OB(图略),
∵△AOC 是等边三角形,
∴∠AOC = 60°,
∵点 A,B,C 是正多边形的顶点,O 是正多边形的中心,
∴∠AOB = ∠BOC = $\frac{1}{2}$∠AOC = 30°,即正多边形的中心角的度数为 30°,设这个正多边形为正 n 边形,
∴$\frac{360°}{n}$ = 30°,
∴n = 12。故选 C。
∵△AOC 是等边三角形,
∴∠AOC = 60°,
∵点 A,B,C 是正多边形的顶点,O 是正多边形的中心,
∴∠AOB = ∠BOC = $\frac{1}{2}$∠AOC = 30°,即正多边形的中心角的度数为 30°,设这个正多边形为正 n 边形,
∴$\frac{360°}{n}$ = 30°,
∴n = 12。故选 C。
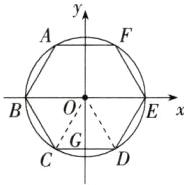
3. [2024 天津河东期末]如图,正六边形 ABCDEF 的中心为原点 O,顶点 B,E 在 x 轴上,半径为 4,则顶点 D 的坐标为( )

A. $(2,2\sqrt {3})$
B. $(2,-2\sqrt {3})$
C. $(2,-4)$
D. $(2\sqrt {3},-4)$

A. $(2,2\sqrt {3})$
B. $(2,-2\sqrt {3})$
C. $(2,-4)$
D. $(2\sqrt {3},-4)$
答案:
B 如图,连接 OD,OC,设 CD 交 y 轴于 G,易知 OG⊥CD。
∵正六边形 ABCDEF 的中心为原点 O,
∴∠COD = $\frac{360°}{6}$ = 60°,
∵OC = OD = 4,OG⊥CD,
∴∠GOD = $\frac{∠COD}{2}$ = 30°,
∴DG = 2,
∴OG = $\sqrt{OD² - DG²}$ = $2\sqrt{3}$,
∴点 D 的坐标为(2,$-2\sqrt{3}$)。故选 B。
B 如图,连接 OD,OC,设 CD 交 y 轴于 G,易知 OG⊥CD。
∵正六边形 ABCDEF 的中心为原点 O,

∴∠COD = $\frac{360°}{6}$ = 60°,
∵OC = OD = 4,OG⊥CD,
∴∠GOD = $\frac{∠COD}{2}$ = 30°,
∴DG = 2,
∴OG = $\sqrt{OD² - DG²}$ = $2\sqrt{3}$,
∴点 D 的坐标为(2,$-2\sqrt{3}$)。故选 B。
4. 新数学文化 刘徽是中国古代卓越的数学家之一,他在《九章算术》中提出了“割圆术”,即用内接或外切正多边形逐步逼近圆来近似计算圆的面积.如图,设⊙O 的半径为 2,若用⊙O 的内接正六边形的面积来近似估计⊙O 的面积,则⊙O 的面积约为____(结果保留根号).


答案:
答案 $6\sqrt{3}$
解析 如图,连接 OA、OB,由题意可得∠AOB = 360°÷6 = 60°。
∵OA = OB = 2,

∴△OAB 为等边三角形,
∴AB = 2。过点 O 作 OM⊥AB 于点 M,则 AM = BM = 1。
在 Rt△AOM 中,OM = $\sqrt{2² - 1²}$ = $\sqrt{3}$,
∴$S_{△AOB}$ = $\frac{1}{2}$×2×$\sqrt{3}$ = $\sqrt{3}$,
∴⊙O 的面积约为 $6S_{△AOB}$ = $6\sqrt{3}$。
答案 $6\sqrt{3}$
解析 如图,连接 OA、OB,由题意可得∠AOB = 360°÷6 = 60°。
∵OA = OB = 2,

∴△OAB 为等边三角形,
∴AB = 2。过点 O 作 OM⊥AB 于点 M,则 AM = BM = 1。
在 Rt△AOM 中,OM = $\sqrt{2² - 1²}$ = $\sqrt{3}$,
∴$S_{△AOB}$ = $\frac{1}{2}$×2×$\sqrt{3}$ = $\sqrt{3}$,
∴⊙O 的面积约为 $6S_{△AOB}$ = $6\sqrt{3}$。
5. 学科特色教材变式 P108 习题 T1 求半径为 2 的圆的内接正三角形,正方形,正六边形的边长、边心距、中心角和面积.将结果填写在表中:

正三角形:边长

正三角形:边长
$2\sqrt{3}$
,边心距1
,中心角120°
,面积$3\sqrt{3}$
;正方形:边长$2\sqrt{2}$
,边心距$\sqrt{2}$
,中心角90°
,面积8
;正六边形:边长2
,边心距$\sqrt{3}$
,中心角60°
,面积$6\sqrt{3}$
答案:
解析 结果如下表:
正圆的多边内接形 边长 边心距 中心角 面积
正三角形 $2\sqrt{3}$ 1 120° $3\sqrt{3}$
正方形 $2\sqrt{2}$ $\sqrt{2}$ 90° 8
正六边形 2 $\sqrt{3}$ 60° $6\sqrt{3}$
正圆的多边内接形 边长 边心距 中心角 面积
正三角形 $2\sqrt{3}$ 1 120° $3\sqrt{3}$
正方形 $2\sqrt{2}$ $\sqrt{2}$ 90° 8
正六边形 2 $\sqrt{3}$ 60° $6\sqrt{3}$
6. 如图,已知⊙O 和⊙O 上的一点 A,请完成下列任务:
(1)用尺规作⊙O 的内接正六边形 ABCDEF.
(2)连接 BF,CE,判断四边形 BCEF 的形状并加以证明.

(1)用尺规作⊙O 的内接正六边形 ABCDEF.
(2)连接 BF,CE,判断四边形 BCEF 的形状并加以证明.

答案:
解析 (1)如图 1,首先作直径 AD,然后分别以 A,D 为圆心,OA 长为半径画弧,交⊙O 于点 B,F,C,E,连接 AB,BC,CD,DE,EF,AF,则正六边形 ABCDEF 即为所求。


(2)四边形 BCEF 是矩形。证明:如图 2,连接 OE,
∵六边形 ABCDEF 是正六边形,
∴AB = AF = DE = DC = FE = BC,
∴$\overset{\frown}{AB}$ = $\overset{\frown}{AF}$ = $\overset{\frown}{DE}$ = $\overset{\frown}{DC}$,
∴$\overset{\frown}{BF}$ = $\overset{\frown}{CE}$,
∴BF = CE,
∴四边形 BCEF 是平行四边形。
∵六边形 ABCDEF 为正六边形,
∴∠EDC = ∠FED = $\frac{(6 - 2)×180°}{6}$ = 120°。
∵DE = DC,
∴∠DEC = ∠DCE = 30°,
∴∠CEF = ∠DEF - ∠CED = 90°,
∴四边形 BCEF 是矩形。
解析 (1)如图 1,首先作直径 AD,然后分别以 A,D 为圆心,OA 长为半径画弧,交⊙O 于点 B,F,C,E,连接 AB,BC,CD,DE,EF,AF,则正六边形 ABCDEF 即为所求。


(2)四边形 BCEF 是矩形。证明:如图 2,连接 OE,
∵六边形 ABCDEF 是正六边形,
∴AB = AF = DE = DC = FE = BC,
∴$\overset{\frown}{AB}$ = $\overset{\frown}{AF}$ = $\overset{\frown}{DE}$ = $\overset{\frown}{DC}$,
∴$\overset{\frown}{BF}$ = $\overset{\frown}{CE}$,
∴BF = CE,
∴四边形 BCEF 是平行四边形。
∵六边形 ABCDEF 为正六边形,
∴∠EDC = ∠FED = $\frac{(6 - 2)×180°}{6}$ = 120°。
∵DE = DC,
∴∠DEC = ∠DCE = 30°,
∴∠CEF = ∠DEF - ∠CED = 90°,
∴四边形 BCEF 是矩形。
7. [2023 四川内江中考,★☆]如图,正六边形 ABCDEF 内接于⊙O,点 P 在$\overset{\frown }{AB}$上,点 Q 是$\overset{\frown }{DE}$的中点,则∠CPQ 的度数为( )

A. $30^{\circ }$
B. $45^{\circ }$
C. $36^{\circ }$
D. $60^{\circ }$

A. $30^{\circ }$
B. $45^{\circ }$
C. $36^{\circ }$
D. $60^{\circ }$
答案:
B 如图,连接 OC,OD,OQ,OE,

∵六边形 ABCDEF 是正六边形,
∴∠COD = ∠DOE = $\frac{360°}{6}$ = 60°,
∵Q 是$\overset{\frown}{DE}$的中点,
∴∠DOQ = ∠EOQ = $\frac{1}{2}$∠DOE = 30°,
∴∠COQ = ∠COD + ∠DOQ = 90°,
∴∠CPQ = $\frac{1}{2}$∠COQ = 45°。故选 B。
B 如图,连接 OC,OD,OQ,OE,

∵六边形 ABCDEF 是正六边形,
∴∠COD = ∠DOE = $\frac{360°}{6}$ = 60°,
∵Q 是$\overset{\frown}{DE}$的中点,
∴∠DOQ = ∠EOQ = $\frac{1}{2}$∠DOE = 30°,
∴∠COQ = ∠COD + ∠DOQ = 90°,
∴∠CPQ = $\frac{1}{2}$∠COQ = 45°。故选 B。
8. [2024 山东济宁中考,★☆]如图,边长为 2 的正六边形 ABCDEF 内接于⊙O,则它的内切圆半径为( )

A. 1
B. 2
C. $\sqrt {2}$
D. $\sqrt {3}$

A. 1
B. 2
C. $\sqrt {2}$
D. $\sqrt {3}$
答案:
D 如图,连接 OA,OB,过点 O 作 OG⊥AB 于 G:

∵六边形 ABCDEF 是圆的内接正六边形,且边长为 2,
∴∠AOB = $\frac{360°}{6}$ = 60°,AB = 2,
又
∵OA = OB,
∴△OAB 为等边三角形,
∴OA = AB = 2,
∵OG⊥AB,
∴∠AOG = $\frac{1}{2}$∠AOB = $\frac{1}{2}$×60° = 30°,
∴在 Rt△OAG 中,AG = $\frac{1}{2}$OA = 1,
由勾股定理可得 OG = $\sqrt{3}$,
易知 OG 为正六边形 ABCDEF 的内切圆半径,
∴正六边形 ABCDEF 的内切圆半径为 $\sqrt{3}$。
D 如图,连接 OA,OB,过点 O 作 OG⊥AB 于 G:

∵六边形 ABCDEF 是圆的内接正六边形,且边长为 2,
∴∠AOB = $\frac{360°}{6}$ = 60°,AB = 2,
又
∵OA = OB,
∴△OAB 为等边三角形,
∴OA = AB = 2,
∵OG⊥AB,
∴∠AOG = $\frac{1}{2}$∠AOB = $\frac{1}{2}$×60° = 30°,
∴在 Rt△OAG 中,AG = $\frac{1}{2}$OA = 1,
由勾股定理可得 OG = $\sqrt{3}$,
易知 OG 为正六边形 ABCDEF 的内切圆半径,
∴正六边形 ABCDEF 的内切圆半径为 $\sqrt{3}$。
查看更多完整答案,请扫码查看


