第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1.「2025 湖北武汉新洲月考」已知$\odot O$的半径为3,P为$\odot O$所在平面内某直线l上一点,$OP = 3$,则过点P的直线PQ与$\odot O$的公共点个数为(
A.1或2
B.2
C.0
D.1
A
)A.1或2
B.2
C.0
D.1
答案:
A
∵⊙O的半径为3,P为⊙O所在平面内某直线l上一点,OP = 3,
∴直线l与圆相切或相交,故公共点的个数为1或2。故选A。
∵⊙O的半径为3,P为⊙O所在平面内某直线l上一点,OP = 3,
∴直线l与圆相切或相交,故公共点的个数为1或2。故选A。
2.「2025 江苏扬州邗江月考」已知直线l与$\odot O$相离,圆心O到直线l的距离为5 cm,则$\odot O$的半径可能为(
A.4 cm
B.5 cm
C.6 cm
D.7 cm
A
)A.4 cm
B.5 cm
C.6 cm
D.7 cm
答案:
A 设圆的半径为r,圆心O到直线l的距离为d,
∵直线l与⊙O相离,
∴d>r,又
∵圆心O到直线l的距离为5cm,
∴r<5cm。故选A。
∵直线l与⊙O相离,
∴d>r,又
∵圆心O到直线l的距离为5cm,
∴r<5cm。故选A。
3.「2024 江苏南京玄武月考」已知点$A(3,4)$,若以点A为圆心,3个单位长度为半径作圆,则$\odot A$与x轴
相离
,$\odot A$与y轴相切
.
答案:
答案 相离;相切
解析
∵A(3,4),
∴点A到x轴的距离为4>3,点A到y轴的距离为3 = 3,
∴⊙A与x轴相离,⊙A与y轴相切。
解析
∵A(3,4),
∴点A到x轴的距离为4>3,点A到y轴的距离为3 = 3,
∴⊙A与x轴相离,⊙A与y轴相切。
4.「2024 福建福州台江月考」如图,$∠AOB = 30^{\circ}$,$OM = 6$,那么以M为圆心,4为半径的圆与射线OA的位置关系是____.
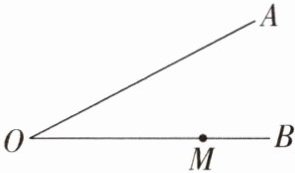

答案:
答案 相交
解析 如图,过M作MN⊥OA于点N,
∵∠AOB = 30°,OM = 6,
∴MN = $\frac{1}{2}$MO = $\frac{1}{2}$×6 = 3<4,
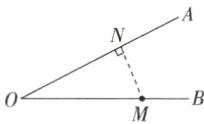
∴⊙M与射线OA相交。
答案 相交
解析 如图,过M作MN⊥OA于点N,
∵∠AOB = 30°,OM = 6,
∴MN = $\frac{1}{2}$MO = $\frac{1}{2}$×6 = 3<4,

∴⊙M与射线OA相交。
5.「2024 甘肃兰州城关期末,」已知$\odot O的半径是一元二次方程x^{2}-7x + 12 = 0$的一个根,圆心O到直线l的距离$d = 3$,则直线l与$\odot O$的位置关系是(
A.相交
B.相切
C.相离或相切
D.相交或相切
D
)A.相交
B.相切
C.相离或相切
D.相交或相切
答案:
D
∵x²−7x + 12 = 0,
∴x₁ = 3,x₂ = 4,设⊙O的半径为r,
∵⊙O的半径为一元二次方程x²−7x + 12 = 0的根,
∴r = 3或r = 4,
∵d = 3,
∴当r = 3时,d = r,此时直线l与⊙O的位置关系是相切,当r = 4时,d<r,此时直线l与⊙O的位置关系是相交。故选D。
∵x²−7x + 12 = 0,
∴x₁ = 3,x₂ = 4,设⊙O的半径为r,
∵⊙O的半径为一元二次方程x²−7x + 12 = 0的根,
∴r = 3或r = 4,
∵d = 3,
∴当r = 3时,d = r,此时直线l与⊙O的位置关系是相切,当r = 4时,d<r,此时直线l与⊙O的位置关系是相交。故选D。
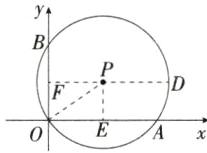
6.「2024 河南许昌二模,」如图,平面直角坐标系中,$\odot P经过三点A(8,0)$,$O(0,0)$,$B(0,6)$,点D是$\odot P$上的一动点.当点D到弦OB的距离最大时,点D的坐标是( )

A.$(9,3)$
B.$(9,6)$
C.$(10,3)$
D.$(10,6)$

A.$(9,3)$
B.$(9,6)$
C.$(10,3)$
D.$(10,6)$
答案:
A
∵点A(8,0),O(0,0),B(0,6),
∴OA = 8,OB = 6,
如图,过点P作PE⊥OA于点E,作PF⊥OB于点F,延长FP交⊙P于点D,连接OP,此时点D到弦OB的距离最大,易得四边形PFOE是矩形,
∴PF = OE = $\frac{1}{2}$OA = 4,OF = EP = $\frac{1}{2}$OB = 3,
∴OP = PD = $\sqrt{EP² + OE²}$ = 5,
∴点D到弦OB的距离最大为PF + PD = 4 + 5 = 9,
∴点D的坐标为(9,3)。
A
∵点A(8,0),O(0,0),B(0,6),
∴OA = 8,OB = 6,
如图,过点P作PE⊥OA于点E,作PF⊥OB于点F,延长FP交⊙P于点D,连接OP,此时点D到弦OB的距离最大,易得四边形PFOE是矩形,
∴PF = OE = $\frac{1}{2}$OA = 4,OF = EP = $\frac{1}{2}$OB = 3,
∴OP = PD = $\sqrt{EP² + OE²}$ = 5,
∴点D到弦OB的距离最大为PF + PD = 4 + 5 = 9,
∴点D的坐标为(9,3)。

7.「2024 上海崇明二模,」已知在$Rt△ABC$中,$∠C = 90^{\circ}$,$AC = 12$,$BC = 5$,若以C为圆心,r为半径的圆C与边AB有交点,那么r的取值范围是( )
A.$5≤r≤12或r= \frac{60}{13}$
B.$5 < r < 12$
C.$\frac{60}{13} < r < 12$
D.$\frac{60}{13}≤r≤12$
A.$5≤r≤12或r= \frac{60}{13}$
B.$5 < r < 12$
C.$\frac{60}{13} < r < 12$
D.$\frac{60}{13}≤r≤12$
答案:
D 作CD⊥AB于D,如图,

∵∠ACB = 90°,AC = 12,BC = 5,
∴AB = $\sqrt{AC² + BC²}$ = 13,
∵$\frac{1}{2}$CD·AB = $\frac{1}{2}$BC·AC,
∴CD = $\frac{60}{13}$,
∴以C为圆心,r为半径作的圆与斜边AB有公共点时,r的取值范围为$\frac{60}{13}$≤r≤12。故选D。
D 作CD⊥AB于D,如图,

∵∠ACB = 90°,AC = 12,BC = 5,
∴AB = $\sqrt{AC² + BC²}$ = 13,
∵$\frac{1}{2}$CD·AB = $\frac{1}{2}$BC·AC,
∴CD = $\frac{60}{13}$,
∴以C为圆心,r为半径作的圆与斜边AB有公共点时,r的取值范围为$\frac{60}{13}$≤r≤12。故选D。
8.「2024 四川绵阳安州期末,」如图所示的是两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB与小圆有公共点,则弦AB的取值范围是

8≤AB≤10
.
答案:
答案 8≤AB≤10
解析
∵大圆的弦AB与小圆有公共点,
∴AB与小圆相切或相交,当AB是大圆的直径时AB的值最大,最大值为10。当AB与小圆相切时AB的值最小,
∵小圆的半径为3,大圆的半径为5,
∴此时AB = 2×$\sqrt{5²−3²}$ = 8,
∴8≤AB≤10。
解析
∵大圆的弦AB与小圆有公共点,
∴AB与小圆相切或相交,当AB是大圆的直径时AB的值最大,最大值为10。当AB与小圆相切时AB的值最小,
∵小圆的半径为3,大圆的半径为5,
∴此时AB = 2×$\sqrt{5²−3²}$ = 8,
∴8≤AB≤10。
9.「2025 甘肃武威凉州期末,」如图,已知$\odot P$的半径为3,圆心P在抛物线$y = \frac{1}{3}x^{2}-1$上运动,当$\odot P$与y轴相切时,圆心P的坐标为

(3,2)或(−3,2)
.
答案:
答案 (3,2)或(−3,2)
解析
∵⊙P与y轴相切,⊙P的半径为3,
∴点P到y轴的距离等于3,
∴点P的横坐标为3或−3,
当x = 3时,代入可得y = $\frac{1}{3}$×3²−1 = 2,此时点P的坐标为(3,2);
当x = −3时,代入可得y = $\frac{1}{3}$×(−3)²−1 = 2,此时点P的坐标为(−3,2)。
综上可知,点P的坐标为(3,2)或(−3,2)。
故答案为(3,2)或(−3,2)。
解析
∵⊙P与y轴相切,⊙P的半径为3,
∴点P到y轴的距离等于3,
∴点P的横坐标为3或−3,
当x = 3时,代入可得y = $\frac{1}{3}$×3²−1 = 2,此时点P的坐标为(3,2);
当x = −3时,代入可得y = $\frac{1}{3}$×(−3)²−1 = 2,此时点P的坐标为(−3,2)。
综上可知,点P的坐标为(3,2)或(−3,2)。
故答案为(3,2)或(−3,2)。
10.「2024 北京海淀期末,」如图,在平面直角坐标系xOy中,以点$A(\sqrt{2},0)$为圆心,1为半径画圆,将$\odot A$绕点O逆时针旋转$α(0^{\circ} < α < 180^{\circ})得到\odot A'$,使得$\odot A'$与y轴相切,则α的度数是____.


答案:
答案 45°或135°
解析 如图1,点A'在第一象限,设⊙A'与y轴相切于点B,连接OA'、BA',由相切可知OB⊥A'B,
∴∠A'BO = 90°,
∵A($\sqrt{2}$,0),
∴OA = $\sqrt{2}$,由旋转得OA' = OA = $\sqrt{2}$,
∵⊙A的半径为1,
∴⊙A'的半径为1,
∴A'B = 1,
∴OB = $\sqrt{OA'²−A'B²}$ = $\sqrt{(\sqrt{2})^{2}−1^{2}}$ = 1,
∴A'B = OB,
∴∠BOA' = ∠BA'O = 45°,
∴α = ∠AOA' = 90°−45° = 45°;
如图2,点A'在第二象限,设⊙A'与y轴相切于点C,连接OA'、CA',由相切可知OC⊥A'C,
∴∠A'CO = 90°,
∵OA' = OA = $\sqrt{2}$,A'C = 1,
∴OC = $\sqrt{OA'²−A'C²}$ = $\sqrt{(\sqrt{2})^{2}−1^{2}}$ = 1,
∴A'C = OC,
∴∠COA' = ∠CA'O = 45°,
∴α = ∠AOA' = 90° + 45° = 135°。
综上,α的度数为45°或135°。


答案 45°或135°
解析 如图1,点A'在第一象限,设⊙A'与y轴相切于点B,连接OA'、BA',由相切可知OB⊥A'B,
∴∠A'BO = 90°,
∵A($\sqrt{2}$,0),
∴OA = $\sqrt{2}$,由旋转得OA' = OA = $\sqrt{2}$,
∵⊙A的半径为1,
∴⊙A'的半径为1,
∴A'B = 1,
∴OB = $\sqrt{OA'²−A'B²}$ = $\sqrt{(\sqrt{2})^{2}−1^{2}}$ = 1,
∴A'B = OB,
∴∠BOA' = ∠BA'O = 45°,
∴α = ∠AOA' = 90°−45° = 45°;
如图2,点A'在第二象限,设⊙A'与y轴相切于点C,连接OA'、CA',由相切可知OC⊥A'C,
∴∠A'CO = 90°,
∵OA' = OA = $\sqrt{2}$,A'C = 1,
∴OC = $\sqrt{OA'²−A'C²}$ = $\sqrt{(\sqrt{2})^{2}−1^{2}}$ = 1,
∴A'C = OC,
∴∠COA' = ∠CA'O = 45°,
∴α = ∠AOA' = 90° + 45° = 135°。
综上,α的度数为45°或135°。


查看更多完整答案,请扫码查看


