《2025年5年中考3年模拟九年级数学上册人教版》

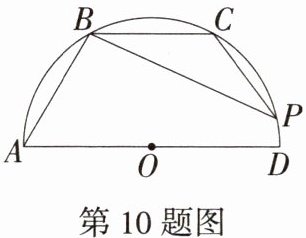
10.特色 多解法「2024海南中考,★☆」如图,AD是半圆O的直径,点B,C在半圆上,且$\overset{\frown}{AB}= \overset{\frown}{BC}= \overset{\frown}{CD}$,点P在$\overset{\frown}{CD}$上,若∠PCB= 130°,则∠PBA等于( )

A.105°
B.100°
C.90°
D.70°

答案：
B 如图，连接OB，OC.
∵AD是半圆O的直径，
∴∠AOD = 180°.
∵$\overset{\frown}{AB}$ = $\overset{\frown}{BC}$ = $\overset{\frown}{CD}$，
∴∠AOB = ∠BOC = ∠COD = 60°.
∵OA = OB = OC，
∴△AOB和△BOC均是等边三角形，
∴∠ABO = ∠CBO = ∠BCO = 60°，
∴∠ABC = ∠ABO + ∠CBO = 120°.

[解法一]
∵∠BPC是$\overset{\frown}{BC}$所对的圆周角，∠BOC是$\overset{\frown}{BC}$所对的圆心角，
∴∠BPC = $\frac{1}{2}$∠BOC = 30°.
∵∠PCB = 130°，
∴∠PBC = 180° - ∠BPC - ∠PCB = 180° - 30° - 130° = 20°，
∴∠ABP = ∠ABC - ∠PBC = 120° - 20° = 100°.故选B.
[解法二] 如图，连接OP.
∵OC = OP，
∴△COP是等腰三角形，
∵∠PCB = 130°，
∴∠OPC = ∠OCP = ∠PCB - ∠BCO = 130° - 60° = 70°，
∴∠COP = 180° - ∠OPC - ∠OCP = 180° - 70° - 70° = 40°，
∴∠PBC = $\frac{1}{2}$∠COP = $\frac{1}{2}$×40° = 20°，
∴∠PBA = ∠ABC - ∠PBC = 120° - 20° = 100°.故选B.

11.「2025浙江杭州萧山期中,★☆」如图,AB为⊙O的直径,点C为圆上一点,若将劣弧AC沿弦AC翻折交AB于点D,连接CD,∠DCA= 44°,则∠BAC的度数为( )

A.23°
B.24°
C.25°
D.26°

答案：
A 如图，连接BC，
∵AB是⊙O的直径，
∴∠ACB = 90°，
∵∠DCA = 44°，

∴∠BCD = 90° - 44° = 46°，根据翻折的性质，知$\overset{\frown}{ABC}$所对的圆周角为∠ADC，
∵$\overset{\frown}{AC}$所对的圆周角为∠B，
∴∠ADC + ∠B = 180°，
∵∠ADC + ∠BDC = 180°，
∴∠B = ∠BDC = $\frac{1}{2}$×(180° - 46°) = 67°，
∴∠BAC = 90° - 67° = 23°.故选A.

12.「2024江苏连云港中考,★☆」如图,AB是圆的直径,∠1、∠2、∠3、∠4的顶点均在AB上方的圆弧上,∠1、∠4的一边分别经过点A、B,则∠1+∠2+∠3+∠4=90°.

答案： 答案 90
解析
∵AB是圆的直径，
∴AB所对的弧是半圆，所对圆心角的度数为180°，
∵∠1、∠2、∠3、∠4所对的弧的和为半圆，
∴∠1 + ∠2 + ∠3 + ∠4 = $\frac{1}{2}$×180° = 90°.

13.「2024山西朔州怀仁期中,★☆」如图,AC,BD是⊙O的两条相交弦,∠ACB= ∠CDB= 60°,AC= 2$\sqrt{3}$,则⊙O的直径是______.

答案：
答案 4
解析 如图，作直径BM，连接CM，
∴∠BCM = 90°，易知∠A = ∠D = ∠M = 60°，
∵∠ACB = 60°，

∴∠ABC = 60°，
∴△ABC是等边三角形，
∴BC = AC = 2$\sqrt{3}$. 在Rt△BCM中，∠M = 60°，
∴∠CBM = 30°，
∴BM = 2CM，
∵BC² + CM² = BM²，
∴(2$\sqrt{3}$)² + CM² = 4CM²，
∴CM = 2（舍负），
∴BM = 4，
∴⊙O的直径是4.

14.「2024浙江湖州南浔期末,★☆」如图,△ABC中,AB= AC,以AB为直径作⊙O,交BC边于点D,交CA的延长线于点E,连接AD,DE.
(1)求证：BD= CD.
(2)若AB= 5,DE= 4,求AD的长.

(1)证明：∵AB是⊙O的直径，∴∠ADB = 90°，∴AD⊥BD，又∵AB = AC，∴BD = CD.
(2)∵AB = 5，∴AC = AB = 5，∴∠B = ∠C. ∵∠B = ∠E，∴∠E = ∠C，∴DC = DE = 4. ∵∠ADB = 90°，∴∠ADC = 90°，∴AD = $\sqrt{AC^{2}-CD^{2}}$ = $\sqrt{5^{2}-4^{2}}$ = 3.

答案： 解析 （1）证明：
∵AB是⊙O的直径，
∴∠ADB = 90°，
∴AD⊥BD，又
∵AB = AC，
∴BD = CD.
（2）
∵AB = 5，
∴AC = AB = 5，
∴∠B = ∠C.
∵∠B = ∠E，
∴∠E = ∠C，
∴DC = DE = 4.
∵∠ADB = 90°，
∴∠ADC = 90°，
∴AD = $\sqrt{AC^{2}-CD^{2}}$ = $\sqrt{5^{2}-4^{2}}$ = 3.

15.新 课标 推理能力「2025湖北荆州期中」如图,AB为⊙O的直径,点C,D为直径AB同侧圆上的点,且点D为$\overset{\frown}{AC}$的中点,过点D作DE⊥AB于点E,交AC于点G,延长DE,交⊙O于点F.
(1)如图①,若∠BAC= 30°,求证：$\overset{\frown}{CD}= \overset{\frown}{BC}$.
(2)如图②,若AC= 12,BE= 9,求⊙O的半径.

答案：
解析 （1）证明：如图①，连接OC，OD，
∵∠BAC = 30°，
∴∠BOC = 2∠BAC = 60°，
∴∠AOC = 180° - 60° = 120°，
∵点D为$\overset{\frown}{AC}$的中点，
∴$\overset{\frown}{AD}$ = $\overset{\frown}{DC}$，
∴∠AOD = ∠COD = 60°，
∴∠COD = ∠COB，
∴$\overset{\frown}{CD}$ = $\overset{\frown}{BC}$.


（2）如图②，连接OF，
∵DE⊥AB，AB为⊙O的直径，
∴$\overset{\frown}{AD}$ = $\overset{\frown}{AF}$，DE = EF，
∵$\overset{\frown}{AD}$ = $\overset{\frown}{DC}$，
∴$\overset{\frown}{AD}$ + $\overset{\frown}{DC}$ = $\overset{\frown}{AD}$ + $\overset{\frown}{AF}$，
∴$\overset{\frown}{AC}$ = $\overset{\frown}{DF}$，
∴DF = AC = 12，
∴EF = 6，设⊙O的半径为r，则OE = BE - OB = 9 - r，在Rt△EOF中，EO² + EF² = OF²，即(9 - r)² + 6² = r²，解得r = 6.5，
∴⊙O的半径为6.5.