《2025年5年中考3年模拟九年级数学上册人教版》

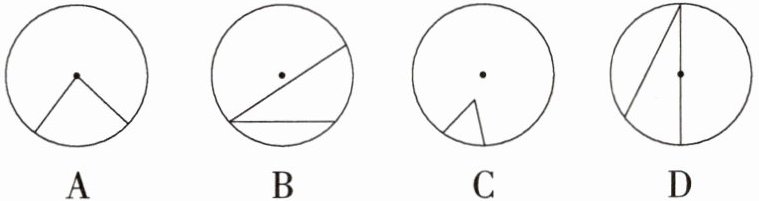
1. [2024 福建福州仓山月考]下列图形中表示的角是圆心角的是 (A)

答案： A 四个选项中只有选项 A 中的图形表示的角是圆心角.故选 A.

2. [学科特色 教材变式 P85T2]如图,A、B、C、D 都是$\odot O$上的点,若$CD= BD$,$∠AOC= 108^{\circ }$,则$∠AOD= $ (B)

A.$140^{\circ }$
B.$144^{\circ }$
C.$146^{\circ }$
D.$150^{\circ }$

答案： B $\because ∠AOC = 108^{\circ}$，$\therefore ∠BOC = 180^{\circ} - 108^{\circ} = 72^{\circ}$，$\because CD = BD$，$\therefore ∠BOD = ∠COD = \frac{1}{2}∠BOC = 36^{\circ}$，$\therefore ∠AOD = ∠AOC + ∠COD = 108^{\circ} + 36^{\circ} = 144^{\circ}$.故选 B.

3. [2025 江苏扬州宝应期中]如图,在$\odot O$中,点 A、B、C 在圆上,且弧 AB 的长等于弧 AC 长的 2 倍,则下列结论正确的是 ( )

A.$AB= 2AC$
B.$AB＞2AC$
C.$AB＜2AC$
D.以上结论都不对

答案：
C 如图，取$\overset{\frown}{AB}$的中点 H，连接 AH、BH，则$\overset{\frown}{AH} = \overset{\frown}{BH}$，$\because$弧 AB 的长等于弧 AC 长的 2 倍，$\therefore \overset{\frown}{AH} = \overset{\frown}{BH} = \overset{\frown}{AC}$，$\therefore AH = BH = AC$，在$\triangle ABH$中，$AH + BH ＞ AB$，$\therefore AB ＜ 2AC$，故选 C.

4. [2025 江苏徐州新沂期中]如图,在$\triangle ABC$中,$AB= AC$,$∠C= 67.5^{\circ }$,以 AB 为直径的半圆与 BC,AC 分别相交于点 D,E,则弧 AE 所对圆心角的度数为 ( )

A.$40^{\circ }$
B.$50^{\circ }$
C.$90^{\circ }$
D.$100^{\circ }$

答案：
C 如图，连接 OE，$\because AB = AC$，$\therefore ∠B = ∠C = 67.5^{\circ}$，$\therefore ∠BAC = 180^{\circ} - 67.5^{\circ} - 67.5^{\circ} = 45^{\circ}$，$\because OA = OE$，$\therefore ∠AEO = ∠BAC = 45^{\circ}$，$\therefore ∠AOE = 180^{\circ} - 2×45^{\circ} = 90^{\circ}$，$\therefore$弧 AE 所对圆心角的度数为$90^{\circ}$，故选 C.

5. [2024 上海长宁二模]如图,已知点 A、B、C、D 都在$\odot O$上,$OB⊥AC$,$BC= CD$,下列说法错误的是 (C)

A.$\overset{\frown }{AB}= \overset{\frown }{BC}$
B.$∠AOD= 3∠BOC$
C.$AC= 2CD$
D.$OC⊥BD$

答案： C A.$\because OB⊥AC$，$\therefore \overset{\frown}{AB} = \overset{\frown}{BC}$，故不符合题意；B.$\because \overset{\frown}{AB} = \overset{\frown}{BC}$，$\therefore ∠AOB = ∠COB$，$\because BC = CD$，$\therefore ∠BOC = ∠DOC$，$\therefore ∠AOD = 3∠BOC$，故不符合题意；C.$\because ∠AOB = ∠BOC = ∠DOC$，$\therefore ∠AOC = ∠BOD$，$\therefore AC = BD$，$\because BD ＜ BC + CD = 2CD$，$\therefore AC ＜ 2CD$，故符合题意；D.$\because OB = OD$，$BC = DC$，$\therefore OC⊥BD$，故不符合题意.故选 C.

6. [2025 江苏南通启东月考]如图,AB 是$\odot O$的直径,$∠BOD= 120^{\circ }$,点 C 为弧 BD 的中点,AC 交 OD 于点 E,$DE= 1$,则 AE 的长为 ( )

A.$2\sqrt {5}$
B.$\sqrt {5}$
C.$2\sqrt {3}$
D.$\sqrt {3}$

答案：
D 如图，连接 OC.$\because ∠DOB = 120^{\circ}$，$\therefore ∠AOD = 60^{\circ}$，$\because$点 C 为$\overset{\frown}{BD}$的中点，$\therefore \overset{\frown}{CD} = \overset{\frown}{BC}$，$\therefore ∠DOC = ∠BOC = 60^{\circ}$，$\therefore ∠DOC = ∠AOD$，$\therefore \overset{\frown}{AD} = \overset{\frown}{CD}$，$\therefore OD⊥AC$，$\therefore ∠AEO = 90^{\circ}$，$\therefore ∠OAE = 30^{\circ}$，$\therefore OE = \frac{1}{2}OA$.设$OA = r$，则$OE = \frac{1}{2}r$，易知$OE = DE$，$\therefore \frac{1}{2}r = 1$，$\therefore r = 2$，即$OA = 2$，$\therefore AE = \sqrt{OA^{2} - OE^{2}} = \sqrt{3}$.故选 D.

7. [2024 河南驻马店汝南期中]如图,点 A 在半圆 O 上,BC 是直径,$\overset{\frown }{AB}= \overset{\frown }{AC}$,若$BC= 3\sqrt {2}$,则 AB 的长为

______.

答案：
答案 3
解析 如图，连接 AC，OA，$\because \overset{\frown}{AB} = \overset{\frown}{AC}$，$\therefore AB = AC$，$∠AOB = ∠AOC = 90^{\circ}$，$\because OA = OB = OC$，$\therefore ∠BAO = ∠CAO = 45^{\circ}$，$\therefore ∠BAC = 90^{\circ}$，$\therefore \triangle ABC$为等腰直角三角形，$\therefore 2AB^{2} = (3\sqrt{2})^{2}$，$\therefore AB = 3$（舍负）.

8. [2025 江苏镇江月考]如图,AB、CD 是$\odot O$的两条弦,AC 与 BD 相交于点 E,$AB= CD$.
(1)求证：$AC= BD$.
(2)连接 BC,作直线 EO,求证：$EO⊥BC$.

答案：
证明
(1)$\because AB = CD$，$\therefore \overset{\frown}{AB} = \overset{\frown}{CD}$，$\therefore \overset{\frown}{AB} + \overset{\frown}{AD} = \overset{\frown}{CD} + \overset{\frown}{AD}$，即$\overset{\frown}{BD} = \overset{\frown}{AC}$，$\therefore AC = BD$.
(2)如图，连接 OB、OC，在$\triangle ABC$和$\triangle DCB$中，$\begin{cases}AB = DC,\\AC = BD,\\BC = BC,\end{cases}$ $\therefore \triangle ABC ≌ \triangle DCB$，$\therefore ∠ACB = ∠DBC$，$\therefore EB = EC$，$\because OB = OC$，$\therefore$点 E、O 都在 BC 的垂直平分线上，$\therefore EO⊥BC$.