第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1.「2025 黑龙江大庆肇源期中」淘气没有圆规,用如图所示的方法成功画出了圆,他画圆时 (
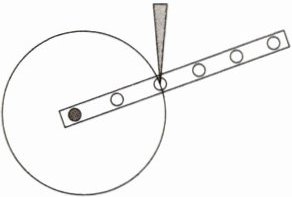
A.保持圆心位置不变
B.保持圆的半径不变
C.保持圆心位置和圆的半径不变
D.圆心的位置可以改变
C
)
A.保持圆心位置不变
B.保持圆的半径不变
C.保持圆心位置和圆的半径不变
D.圆心的位置可以改变
答案:
1.C 淘气画圆时保持圆心位置和圆的半径不变.故选C.
2.「2025 黑龙江大庆期中」把圆规的两脚分开,两脚间的距离是3厘米,再把有针尖的一只脚固定在一点上,把装有铅笔尖的一只脚旋转一周,就画出一个圆,则这个圆的 (
A.半径是3厘米
B.直径是3厘米
C.周长是3π厘米
D.面积是3π平方厘米
A
)A.半径是3厘米
B.直径是3厘米
C.周长是3π厘米
D.面积是3π平方厘米
答案:
2.A
∵两脚间的距离是3厘米,
∴圆的半径为3厘米,
∴直径是6厘米,周长为$6\pi$厘米,面积为$9\pi$平方厘米.故选A.
∵两脚间的距离是3厘米,
∴圆的半径为3厘米,
∴直径是6厘米,周长为$6\pi$厘米,面积为$9\pi$平方厘米.故选A.
3.「2024 江苏无锡江阴月考」下列说法错误的是(
A.直径是圆中最长的弦
B.长度相等的两条弧是等弧
C.面积相等的两个圆是等圆
D.半径相等的两个半圆是等弧
B
)A.直径是圆中最长的弦
B.长度相等的两条弧是等弧
C.面积相等的两个圆是等圆
D.半径相等的两个半圆是等弧
答案:
3.B 只有在同圆或等圆中,长度相等的两条弧才是等弧,故选B.
第一部分答案全解全析D39
拓展解读 等弧的判定
在同圆或等圆中,能够互相重合的弧叫做等弧.
弧从弧度和弧长两个方面进行度量,任意两条长度相等的弧只是弧长相等,弧度不一定相等,故不一定是等弧.
第一部分答案全解全析D39
拓展解读 等弧的判定
在同圆或等圆中,能够互相重合的弧叫做等弧.
弧从弧度和弧长两个方面进行度量,任意两条长度相等的弧只是弧长相等,弧度不一定相等,故不一定是等弧.
4.下面能用来证明“直径是圆中最长的弦”的图形是 (

B
)
答案:
4.B 选项A中,AC是弦,AB是直径,在此图中$AC < AB$,但不能代表所有情况;选项B中,CD是弦(非直径),AB是直径,$CD < OD + OC = AB$,能用来证明“直径是圆中最长的弦”;选项C中,AC不是弦,不能用来证明“直径是圆中最长的弦”;选项D中,CD是弦,AB是直径,在此图中$CD < AB$,但不能代表所有情况.故选B.
5.「2025 浙江杭州期中,★☆」如图,点A、N在半圆O上,四边形ABOC,DNMO均为矩形,$BC= a$,$MD= b$,则a、b的关系为 ( )

A.$a>b$
B.$a= b$
C.$a<b$
D.$a≤b$

A.$a>b$
B.$a= b$
C.$a<b$
D.$a≤b$
答案:
5.B 如图,连接ON、OA,
∵点A、N在半圆上,
∴ $ON = OA$,
∵四边形ABOC,DNMO均为矩形,
∴ $ON = MD$,$OA = BC$,
∴ $BC = MD$,即 $a = b$.故选B.

5.B 如图,连接ON、OA,
∵点A、N在半圆上,
∴ $ON = OA$,
∵四边形ABOC,DNMO均为矩形,
∴ $ON = MD$,$OA = BC$,
∴ $BC = MD$,即 $a = b$.故选B.

6.「★☆」如图,AB是$\odot O$的弦,$OC⊥AB$,垂足为C,$OD// AB$,$OC= \frac {1}{2}OD$,则$∠ABD$的度数为(

A.$90^{\circ }$
B.$95^{\circ }$
C.$100^{\circ }$
D.$105^{\circ }$
D
)
A.$90^{\circ }$
B.$95^{\circ }$
C.$100^{\circ }$
D.$105^{\circ }$
答案:
6.D 连接OB(图略),
∵OB,OD为$\odot O$的半径,
∴ $OB = OD$,
∴ $OC = \frac{1}{2}OD = \frac{1}{2}OB$.在$Rt\triangle OCB$中,由 $OC = \frac{1}{2}OB$ 得 $\angle OBC = 30^{\circ}$.
∵ $OD // AB$,
∴ $\angle BOD = \angle OBC = 30^{\circ}$,
∴ $\angle OBD = \angle ODB = \frac{1}{2}(180^{\circ} - \angle BOD) = 75^{\circ}$,
∴ $\angle ABD = 30^{\circ} + 75^{\circ} = 105^{\circ}$.故选D.
∵OB,OD为$\odot O$的半径,
∴ $OB = OD$,
∴ $OC = \frac{1}{2}OD = \frac{1}{2}OB$.在$Rt\triangle OCB$中,由 $OC = \frac{1}{2}OB$ 得 $\angle OBC = 30^{\circ}$.
∵ $OD // AB$,
∴ $\angle BOD = \angle OBC = 30^{\circ}$,
∴ $\angle OBD = \angle ODB = \frac{1}{2}(180^{\circ} - \angle BOD) = 75^{\circ}$,
∴ $\angle ABD = 30^{\circ} + 75^{\circ} = 105^{\circ}$.故选D.
7.「2025 江苏苏州常熟模拟,★☆」如图,AB是$\odot O$的直径,点C,D在$\odot O$上,$∠BOC= 110^{\circ }$,$AD// OC$,则$∠AOD= $

$40^{\circ}$
.
答案:
7.答案 $40^{\circ}$
解析
∵ $\angle BOC = 110^{\circ}$, $\angle BOC + \angle AOC = 180^{\circ}$,
∴ $\angle AOC = 180^{\circ} - \angle BOC = 180^{\circ} - 110^{\circ} = 70^{\circ}$,
∵ $AD // OC$,
∴ $\angle A = \angle AOC = 70^{\circ}$,
∵ $OD = OA$,
∴ $\angle D = \angle A = 70^{\circ}$,
∴ $\angle AOD = 180^{\circ} - 2\angle A = 180^{\circ} - 2 \times 70^{\circ} = 40^{\circ}$.
解析
∵ $\angle BOC = 110^{\circ}$, $\angle BOC + \angle AOC = 180^{\circ}$,
∴ $\angle AOC = 180^{\circ} - \angle BOC = 180^{\circ} - 110^{\circ} = 70^{\circ}$,
∵ $AD // OC$,
∴ $\angle A = \angle AOC = 70^{\circ}$,
∵ $OD = OA$,
∴ $\angle D = \angle A = 70^{\circ}$,
∴ $\angle AOD = 180^{\circ} - 2\angle A = 180^{\circ} - 2 \times 70^{\circ} = 40^{\circ}$.
8.新课标几何直观 如图,有一个半圆片,点E为圆心,$∠AED= 52^{\circ }$,在平面直角坐标系中,若点A可以沿y轴正半轴上下滑动,同时点B在x轴正半轴上滑动,当$∠OAB= n^{\circ }$时,半圆片上的点D与原点O之间的距离最大,则n的值为( )

A.64
B.52
C.38
D.26

A.64
B.52
C.38
D.26
答案:
8.D 如图,连接OE、OD.易知当点O、E、D共线时,半圆片上的点D与原点O之间的距离最大,此时$\angle AED = \angle EAO + \angle EOA$,在$Rt\triangle AOB$中,因为 $AE = EB$,所以 $EA = EO = EB$,所以 $\angle EAO = \angle EOA$,所以 $n^{\circ} = \frac{1}{2}\angle AED = 26^{\circ}$.故选D.

8.D 如图,连接OE、OD.易知当点O、E、D共线时,半圆片上的点D与原点O之间的距离最大,此时$\angle AED = \angle EAO + \angle EOA$,在$Rt\triangle AOB$中,因为 $AE = EB$,所以 $EA = EO = EB$,所以 $\angle EAO = \angle EOA$,所以 $n^{\circ} = \frac{1}{2}\angle AED = 26^{\circ}$.故选D.

查看更多完整答案,请扫码查看


