第54页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1. 中华优秀传统文化 [2024 四川内江中考]2024 年 6 月 5 日是二十四节气的芒种,二十四节气是中国劳动人民独创的文化遗产,能反映季节的变化,指导农事活动。下面四个选项中的图片分别代表“芒种”“白露”“立夏”“大雪”,其中是中心对称图形的是(
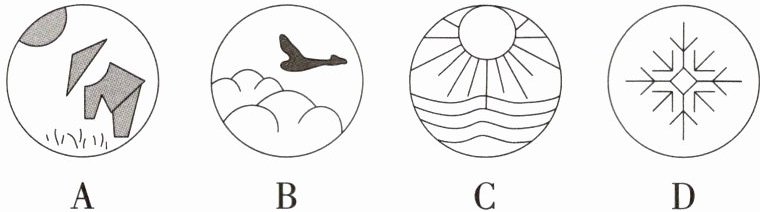
D
)
答案:
1. D
2. [2025 贵州贵阳花溪月考]如图所示的是由 6 个等边三角形组成的中心对称图形,点 A,B,C 是三角形的顶点,D 是边 AC 的中点,则该图形的对称中心是(

A. 点 A
B. 点 B
C. 点 C
D. 点 D
D
)
A. 点 A
B. 点 B
C. 点 C
D. 点 D
答案:
2. D 题图绕点 D 旋转 180°后与原图重合,所以对称中心是点 D。故选 D。
3. [2024 广东中山期中]如图所示的方格纸中,若选择一个标有序号的小正方形涂黑,使其与图中阴影部分组成中心对称图形,则该小正方形的序号是______

②
。
答案:
3. 答案 ②
解析 由中心对称图形的定义可知,将标有序号②的小正方形涂黑后,能够与题图中的阴影部分组成中心对称图形。
解析 由中心对称图形的定义可知,将标有序号②的小正方形涂黑后,能够与题图中的阴影部分组成中心对称图形。
4. [2025 广东汕头潮南期中]下图是一个中心对称图形,A 为对称中心,若∠C = 90°,∠BAC = 60°,BC = 1,则 CC'的长为(

A. $\frac{2\sqrt{3}}{3}$
B. $\frac{4\sqrt{3}}{3}$
C. $\frac{\sqrt{3}}{3}$
D. 4
$\frac{2\sqrt{3}}{3}$
)
A. $\frac{2\sqrt{3}}{3}$
B. $\frac{4\sqrt{3}}{3}$
C. $\frac{\sqrt{3}}{3}$
D. 4
答案:
4. A
∵∠C = 90°, ∠BAC = 60°,
∴∠B = 30°,
∴AB = 2AC。在 Rt△ABC 中,AC² + BC² = AB²,
∵BC = 1,
∴AC² + 1² = 4AC²,
∴AC = $\frac{\sqrt{3}}{3}$。
∵题图是一个中心对称图形,
∴CC' = 2AC = 2 × $\frac{\sqrt{3}}{3}$ = $\frac{2\sqrt{3}}{3}$。故选 A。
∵∠C = 90°, ∠BAC = 60°,
∴∠B = 30°,
∴AB = 2AC。在 Rt△ABC 中,AC² + BC² = AB²,
∵BC = 1,
∴AC² + 1² = 4AC²,
∴AC = $\frac{\sqrt{3}}{3}$。
∵题图是一个中心对称图形,
∴CC' = 2AC = 2 × $\frac{\sqrt{3}}{3}$ = $\frac{2\sqrt{3}}{3}$。故选 A。
5. [★☆☆]在一次数学社团活动中,小明设计了一个社团标识,如图所示,正方形 ABCD 与折线 DE—EF—FB 构成了一个中心对称图形,且 DE⊥EF,AD = 50,DE 比 EF 长 25,那么 EF 的长是______。


答案:
5. 答案 10
解析 如图,连接 BD,与 EF 交于点 O,
∵正方形 ABCD 与折线 DE—EF—FB 构成了中心对称图形,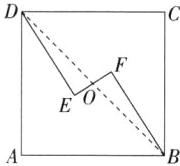
∴OE = $\frac{1}{2}$EF, OD = $\frac{1}{2}$BD,
∵AD = 50,
∴BD = $\sqrt{50^{2} + 50^{2}}$ = 50$\sqrt{2}$,
∴OD = 25$\sqrt{2}$。设 EF = 2x,则 OE = x, DE = 2x + 25,在 Rt△DOE 中,x² + (2x + 25)² = (25$\sqrt{2}$)²,解得 x = 5 或 x = -25(舍去),
∴EF = 5 × 2 = 10。故 EF 的长为 10。
5. 答案 10
解析 如图,连接 BD,与 EF 交于点 O,
∵正方形 ABCD 与折线 DE—EF—FB 构成了中心对称图形,

∴OE = $\frac{1}{2}$EF, OD = $\frac{1}{2}$BD,
∵AD = 50,
∴BD = $\sqrt{50^{2} + 50^{2}}$ = 50$\sqrt{2}$,
∴OD = 25$\sqrt{2}$。设 EF = 2x,则 OE = x, DE = 2x + 25,在 Rt△DOE 中,x² + (2x + 25)² = (25$\sqrt{2}$)²,解得 x = 5 或 x = -25(舍去),
∴EF = 5 × 2 = 10。故 EF 的长为 10。
6. [2024 河北保定期末,★☆☆]知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分。
(1)如图①,直线 m 经过平行四边形 ABCD 对角线的交点 O,则 $S_{四边形AEFB}$______ $S_{四边形DEFC}$(填“>”“<”或“=”)。
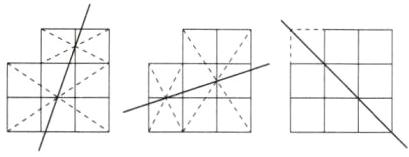
(2)两个正方形按如图②所示的方式摆放,O 为小正方形对角线的交点,求作过点 O 的直线将整个图形分成面积相等的两部分。
(3)八个大小相同的小正方形按如图③所示的方式摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割)。

(1)如图①,直线 m 经过平行四边形 ABCD 对角线的交点 O,则 $S_{四边形AEFB}$______ $S_{四边形DEFC}$(填“>”“<”或“=”)。
(2)两个正方形按如图②所示的方式摆放,O 为小正方形对角线的交点,求作过点 O 的直线将整个图形分成面积相等的两部分。
(3)八个大小相同的小正方形按如图③所示的方式摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割)。

答案:
6. 解析
(1) = 。
(2) 如图所示。

(3) 如图所示。
6. 解析
(1) = 。
(2) 如图所示。

(3) 如图所示。

查看更多完整答案,请扫码查看


