《2025年5年中考3年模拟九年级数学上册人教版》

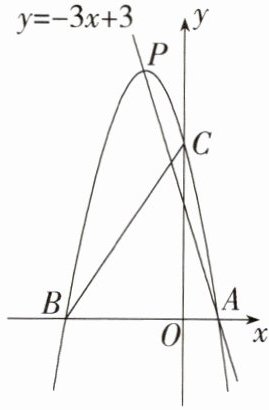
1.「2023四川凉山州中考」如图,已知抛物线与x轴交于A(1,0)和B(-5,0)两点,与y轴交于点C,直线y= -3x+3过抛物线的顶点P.
(1)求抛物线的函数解析式.
(2)若直线x= m(-5＜m＜0)与抛物线交于点E,与直线BC交于点F.
①当EF取得最大值时,求m的值和EF的最大值.
②当△EFC是等腰三角形时,求点E的坐标.

(1)抛物线的函数解析式为y=-(x+2)²+9（或y=-x²-4x+5）.
(2)①当EF取得最大值时，m的值为-5/2，EF的最大值为25/4.
②当△EFC是等腰三角形时，点E的坐标为(-4,5)或(√2-5,-2+6√2)或(-3,8).

答案： 解析
(1)
∵ 抛物线与x轴交于A(1,0)和B(-5,0)两点,
∴ 抛物线的对称轴为直线$x=\frac{1-5}{2}=-2$,在y=-3x+3中,令x=-2得y=9,
∴ 抛物线的顶点坐标为(-2,9),设抛物线的函数解析式为$y=a(x+2)^{2}+9$,将A(1,0)代入得0=9a+9,解得a=-1,
∴ 抛物线的函数解析式为$y=-(x+2)^{2}+9=-x^{2}-4x+5$.
(2)①在$y=-x^{2}-4x+5$中,令x=0得y=5,
∴ C(0,5),由B(-5,0),C(0,5)得直线BC的解析式为y=x+5,
∴ E(m,$-m^{2}-4m+5$),F(m,m+5),
∴ $EF=-m^{2}-4m+5-(m+5)=-m^{2}-5m=-(m+\frac{5}{2})^{2}+\frac{25}{4}$,
∵ -1＜0,
∴ 当$m=-\frac{5}{2}$时,EF取最大值$\frac{25}{4}$,
∴ m的值为$-\frac{5}{2}$,EF的最大值为$\frac{25}{4}$.
②
∵ E(m,$-m^{2}-4m+5$),F(m,m+5),C(0,5),
∴ $EF^{2}=(m^{2}+5m)^{2}$,$EC^{2}=m^{2}+(m^{2}+4m)^{2}$,$FC^{2}=2m^{2}$.若EF=EC,则$(m^{2}+5m)^{2}=m^{2}+(m^{2}+4m)^{2}$,解得m=0(不合题意,舍去)或m=-4,
∴ E(-4,5).
若EF=FC,则$(m^{2}+5m)^{2}=2m^{2}$,解得m=0(舍去)或$m=\sqrt{2}-5$或$m=-\sqrt{2}-5$(不合题意,舍去),
∴ $E(\sqrt{2}-5,-2+6\sqrt{2})$.
若EC=FC,则$m^{2}+(m^{2}+4m)^{2}=2m^{2}$,解得m=0(舍去)或m=-3或m=-5(不合题意,舍去),
∴ E(-3,8).
综上所述,点E的坐标为(-4,5)或$(\sqrt{2}-5,-2+6\sqrt{2})$或(-3,8).

2.「2024安徽淮南田家庵期末」如图,已知点C在y轴正半轴上,OC= 3,将线段OC绕点O顺时针旋转90°到OB的位置,点A的横坐标为方程$x^2-1= 0$的一个解且点A,B在y轴两侧.
(1)求经过A,B,C三点的抛物线的解析式.$y=-x^{2}+2x+3$
(2)在抛物线的对称轴直线l上是否存在点M,使△MAC为直角三角形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.存在，点M的坐标为(1,1)或(1,2)或$(1,\frac{8}{3})$或$(1,-\frac{2}{3})$

答案： 解析
(1)
∵ 点C在y轴正半轴上,OC=3,
∴ C(0,3).由旋转的性质可得OB=OC=3,
∴ B(3,0).
∵ 解方程$x^{2}-1=0$得x=±1,
∴ A(-1,0).设经过A,B,C三点的抛物线的解析式为$y=a(x+1)(x-3)(a≠0)$,把C(0,3)代入,得3=a(0+1)(0-3),解得a=-1,
∴ 抛物线的解析式为$y=-(x+1)(x-3)=-x^{2}+2x+3$.
(2)存在.
在抛物线$y=-x^{2}+2x+3$中,对称轴为直线$x=\frac{-1+3}{2}=1$.设M(1,m),
∴ $AM^{2}=(-1-1)^{2}+(0-m)^{2}=m^{2}+4$,$CM^{2}=(0-1)^{2}+(3-m)^{2}=m^{2}-6m+10$,$AC^{2}=(-1-0)^{2}+(0-3)^{2}=10$.当∠AMC=90°时,$AM^{2}+CM^{2}=AC^{2}$,
∴ $m^{2}+4+m^{2}-6m+10=10$,解得m=1或m=2,
∴ M₁(1,1)或M₂(1,2);
当∠ACM=90°时,$AC^{2}+CM^{2}=AM^{2}$,
∴ $10+m^{2}-6m+10=m^{2}+4$,解得$m=\frac{8}{3}$,
∴ $M_{3}(1,\frac{8}{3})$;
当∠CAM=90°时,$AC^{2}+AM^{2}=CM^{2}$,
∴ $10+m^{2}+4=m^{2}-6m+10$,解得$m=-\frac{2}{3}$,
∴ $M_{4}(1,-\frac{2}{3})$,
综上所述,在抛物线的对称轴直线l上存在点M,使△MAC为直角三角形,点M的坐标为(1,1)或(1,2)或$(1,\frac{8}{3})$或$(1,-\frac{2}{3})$.