第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
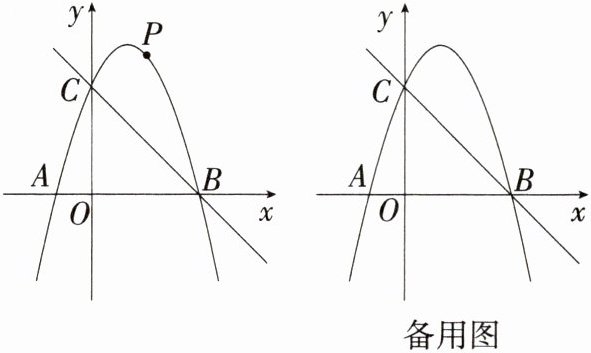
3. [2025山东济南莱芜期末]如图,抛物线y= ax^2+bx+c过点A(-1,0),B(3,0),C(0,3).
(1)求抛物线的表达式.
(2)设P是直线BC上方抛物线上一点,求出△PBC的最大面积及此时点P的坐标.
(3)若点M是线段OC上的一动点,连接AM,求AM+$\frac{\sqrt{2}}{2}$CM的最小值.
(1)求抛物线的表达式.
(2)设P是直线BC上方抛物线上一点,求出△PBC的最大面积及此时点P的坐标.
(3)若点M是线段OC上的一动点,连接AM,求AM+$\frac{\sqrt{2}}{2}$CM的最小值.

答案:
解析
(1)
∵抛物线y=ax²+bx+c过点A(−1,0),B(3,0),
∴抛物线的解析式为y=a(x−3)(x+1),把C(0,3)代入,得3=a(0−3)(0+1),解得a=−1,
故抛物线的解析式为y=−(x−3)(x+1)=−x²+2x+3.
(2)设直线BC的解析式为y=kx+n(k≠0),
将B(3,0),C(0,3)代入,得{3k + n = 0,n = 3,}解得{k = -1,n = 3,}
∴直线BC的解析式为y=−x+3,
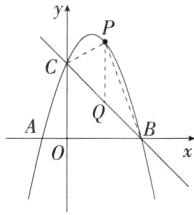
如图,连接PC,PB,过点P作y轴的平行线,交BC于Q,设P(m,−m²+2m+3),则Q(m,−m+3),
∴PQ=−m²+3m,
∴S△PBC=S△PCQ+S△BPQ=$\frac{1}{2}$PQ×(3 - 0)=-$\frac{3}{2}$(m - $\frac{3}{2}$)² + $\frac{27}{8}$,
由此可得,当m=$\frac{3}{2}$时,S△PBC的最大值为$\frac{27}{8}$,
∵当m=$\frac{3}{2}$时,−m²+2m+3=$\frac{15}{4}$,
∴P($\frac{3}{2}$,$\frac{15}{4}$).
(3)
∵B(3,0),C(0,3),∠COB=90°,
∴△COB为等腰直角三角形,
∴∠OCB=45°.
如图,过点M作MH⊥BC于点H,易得△CMH为等腰直角三角形,
∴MH=$\frac{\sqrt{2}}{2}$CM,
∴AM+$\frac{\sqrt{2}}{2}$CM=AM+MH,
∵M为线段OC上的动点,
∴H为线段BC上的动点,
过点A作AH'⊥BC于H',AH'交OC于M',
当A,M,H三点共线,且AH⊥BC,即M在M'处,H在H'处时,AM+$\frac{\sqrt{2}}{2}$CM有最小值,为AH'的长.
∵∠CBO=45°,∠AH'B=90°,
∴△AH'B为等腰直角三角形,
∴AH'=$\frac{\sqrt{2}}{2}$AB=2$\sqrt{2}$,即AM+$\frac{\sqrt{2}}{2}$CM的最小值为2$\sqrt{2}$.

解析
(1)
∵抛物线y=ax²+bx+c过点A(−1,0),B(3,0),
∴抛物线的解析式为y=a(x−3)(x+1),把C(0,3)代入,得3=a(0−3)(0+1),解得a=−1,
故抛物线的解析式为y=−(x−3)(x+1)=−x²+2x+3.
(2)设直线BC的解析式为y=kx+n(k≠0),
将B(3,0),C(0,3)代入,得{3k + n = 0,n = 3,}解得{k = -1,n = 3,}
∴直线BC的解析式为y=−x+3,
如图,连接PC,PB,过点P作y轴的平行线,交BC于Q,设P(m,−m²+2m+3),则Q(m,−m+3),
∴PQ=−m²+3m,
∴S△PBC=S△PCQ+S△BPQ=$\frac{1}{2}$PQ×(3 - 0)=-$\frac{3}{2}$(m - $\frac{3}{2}$)² + $\frac{27}{8}$,
由此可得,当m=$\frac{3}{2}$时,S△PBC的最大值为$\frac{27}{8}$,
∵当m=$\frac{3}{2}$时,−m²+2m+3=$\frac{15}{4}$,
∴P($\frac{3}{2}$,$\frac{15}{4}$).
(3)
∵B(3,0),C(0,3),∠COB=90°,
∴△COB为等腰直角三角形,
∴∠OCB=45°.
如图,过点M作MH⊥BC于点H,易得△CMH为等腰直角三角形,
∴MH=$\frac{\sqrt{2}}{2}$CM,
∴AM+$\frac{\sqrt{2}}{2}$CM=AM+MH,
∵M为线段OC上的动点,
∴H为线段BC上的动点,
过点A作AH'⊥BC于H',AH'交OC于M',
当A,M,H三点共线,且AH⊥BC,即M在M'处,H在H'处时,AM+$\frac{\sqrt{2}}{2}$CM有最小值,为AH'的长.
∵∠CBO=45°,∠AH'B=90°,
∴△AH'B为等腰直角三角形,
∴AH'=$\frac{\sqrt{2}}{2}$AB=2$\sqrt{2}$,即AM+$\frac{\sqrt{2}}{2}$CM的最小值为2$\sqrt{2}$.


4. [2024四川绵阳中考节选]如图,抛物线$y= ax^2+bx+3(a≠0)$与x轴交于点A(-3,0)和B(1,0),与y轴交于点C,连接AC和BC,点P在抛物线上运动,连接AP,BP和CP.
(1)求抛物线的解析式,并写出其顶点坐标.
(2)点P在抛物线上从点A运动到点C的过程中(点P与点A,C不重合),作点P关于x轴的对称点$P_1,$连接$AP_1,CP_1,$记$△ACP_1$的面积为$S_1,△BCP$的面积为$S_2,$若满足$S_1= 3S_2,$求△ABP的面积.

(1)求抛物线的解析式,并写出其顶点坐标.
(2)点P在抛物线上从点A运动到点C的过程中(点P与点A,C不重合),作点P关于x轴的对称点$P_1,$连接$AP_1,CP_1,$记$△ACP_1$的面积为$S_1,△BCP$的面积为$S_2,$若满足$S_1= 3S_2,$求△ABP的面积.

答案:
解析
(1)由题意得y=a(x+3)(x−1)=a(x²+2x−3)=ax²+2ax−3a=ax²+bx+3,
则−3a=3,解得a=−1,
∴抛物线的解析式为y=−x²−2x+3,
∴该抛物线的对称轴为直线x=−1,
∴当x=−1时,y=4,即顶点坐标为(−1,4).
(2)如图,连接PP₁交AC于点E,设PB交y轴于点D,由抛物线表达式知C(0,3).
设P(m,−m²−2m+3),则P₁(m,m²+2m−3),
由A(−3,0),C(0,3)得直线AC的解析式为y=x+3,则E(m,m+3),
同理可得,直线PB的解析式为y=−(m+3)x+m+3,
则D(0,m+3).
由题意得S₁=$\frac{1}{2}$P₁E·OA=$\frac{1}{2}$(m+3 - m²−2m+3)×3=-$\frac{3}{2}$m² - $\frac{3}{2}$m + 9,
S₂=$\frac{1}{2}$CD·(xB - xP)=$\frac{1}{2}$×(3 - m - 3)×(1 - m)=$\frac{1}{2}$m² - $\frac{1}{2}$m.
∵S₁=3S₂,
∴-$\frac{3}{2}$m² - $\frac{3}{2}$m + 9=3($\frac{1}{2}$m² - $\frac{1}{2}$m),解得m=$\sqrt{3}$或m=-$\sqrt{3}$,
∵P在A,C之间的抛物线上,
∴m=-$\sqrt{3}$,
∴P(-$\sqrt{3}$,2$\sqrt{3}$),
∴S△ABP=$\frac{1}{2}$AB×yP=$\frac{1}{2}$×(1 + 3)×2$\sqrt{3}$=4$\sqrt{3}$.

解析
(1)由题意得y=a(x+3)(x−1)=a(x²+2x−3)=ax²+2ax−3a=ax²+bx+3,
则−3a=3,解得a=−1,
∴抛物线的解析式为y=−x²−2x+3,
∴该抛物线的对称轴为直线x=−1,
∴当x=−1时,y=4,即顶点坐标为(−1,4).
(2)如图,连接PP₁交AC于点E,设PB交y轴于点D,由抛物线表达式知C(0,3).
设P(m,−m²−2m+3),则P₁(m,m²+2m−3),
由A(−3,0),C(0,3)得直线AC的解析式为y=x+3,则E(m,m+3),
同理可得,直线PB的解析式为y=−(m+3)x+m+3,
则D(0,m+3).
由题意得S₁=$\frac{1}{2}$P₁E·OA=$\frac{1}{2}$(m+3 - m²−2m+3)×3=-$\frac{3}{2}$m² - $\frac{3}{2}$m + 9,
S₂=$\frac{1}{2}$CD·(xB - xP)=$\frac{1}{2}$×(3 - m - 3)×(1 - m)=$\frac{1}{2}$m² - $\frac{1}{2}$m.
∵S₁=3S₂,
∴-$\frac{3}{2}$m² - $\frac{3}{2}$m + 9=3($\frac{1}{2}$m² - $\frac{1}{2}$m),解得m=$\sqrt{3}$或m=-$\sqrt{3}$,
∵P在A,C之间的抛物线上,
∴m=-$\sqrt{3}$,
∴P(-$\sqrt{3}$,2$\sqrt{3}$),
∴S△ABP=$\frac{1}{2}$AB×yP=$\frac{1}{2}$×(1 + 3)×2$\sqrt{3}$=4$\sqrt{3}$.

查看更多完整答案,请扫码查看


