《2025年5年中考3年模拟九年级数学上册人教版》

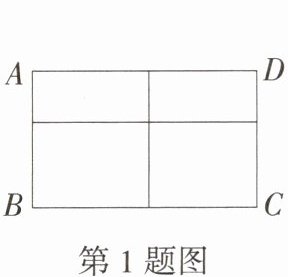
1. [2025黑龙江大庆月考]用总长度为12m的不锈钢材料设计成如图所示的外观为矩形的框架,所有横档和竖档分别与AD,AB平行,则矩形框架ABCD的最大面积为(A)
A.4m²
B.6m²
C.8m²
D.12m²

答案： 1.A　设AB的长为x m，则$AD=\frac{12 - 3x}{3}=(4 - x)m$，
$\therefore S_{矩形框架ABCD}=AB\cdot AD=-x^{2}+4x=-(x - 2)^{2}+4$，当x = 2时，S取得最大值，为4，
∴矩形框架ABCD的最大面积为4m².故选A.

2. [2024安徽六安霍邱期中]如图所示的是一个长为20m,宽为16m的矩形花园,根据需要将它的长缩短xm,宽增加xm,要想使修改后的花园面积达到最大,则x应为(C)

A.1
B.1.5
C.2
D.4

答案： 2.C　设修改后的花园面积为S m²，由题图可得S = (20 - x)(16 + x)=-(x - 2)² + 324，
∴当x = 2时，S取得最大值，为324.故选C.

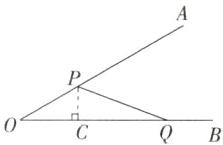
3. 如图,要在夹角为30°的两条小路OA与OB形成的角状空地上建一个三角形花坛,分别在边OA和边OB上取点P和点Q,并扎起篱笆将花坛保护起来(篱笆的厚度忽略不计).若OP和OQ两段篱笆的总长为60m,则该花坛(△POQ)面积的最大值为$______m^2.$

答案：
3.答案　225
解析　如图，过P作PC⊥OB于点C，设OP的长为x m，△POQ的面积为S m²，则OQ的长为(60 - x)m，
∵∠POQ = 30°，
∴$PC=\frac{1}{2}OP=\frac{1}{2}x m$，
∴$S=\frac{1}{2}×\frac{1}{2}x\cdot(60 - x)=-\frac{1}{4}(x - 30)^{2}+225(0 ＜ x ＜ 60)$，
∴当x = 30时，S取得最大值，为225，即当OP的长为30m时，△POQ的面积最大，为225m².

4. [2024甘肃定西期中]在边长为6cm的正方形ABCD中,点E,F,G,H分别按A→B,B→C,C→D,D→A的方向同时出发,以1cm/s的速度匀速运动.写出四边形EFGH的面积$S(cm^2)$关于运动时间t(s)变化的函数关系式$S=2(t-3)^2+18$,并求运动3秒时,四边形EFGH的面积最小,最小值是18$cm^2$.

答案： 4.解析　由题意可知AE = t cm，则EB = (6 - t)cm，则$S = 6^{2}-\frac{1}{2}t(6 - t)×4=2(t - 3)^{2}+18$，
∵0≤t≤6，2＞0，
∴当t = 3时，S取得最小值，此时S = 18，
∴运动3秒时，四边形EFGH的面积最小，最小值是18cm².

5. [2025山西大同期中]某年教师节的主题是“大力弘扬教育家精神,加快建设教育强国”,为庆祝节日,学校为教师定制了水杯,下图是定制的水杯包装盒的表面展开图,设包装盒的高为xcm.
(1)若此包装盒的容积为$1500cm^3,$请列出关于x的方程,并求出x的值.
列出的方程为15x(20 - x)=1500，x的值为10.
(2)是否存在这样的x,使得此包装盒的容积为$1560cm^3？$若存在,请求出相应的x的值；若不存在,请说明理由.
不存在，理由：假设存在这样的x，则15x(20 - x)=1560，整理得x² - 20x + 104 = 0.∵Δ = (-20)² - 4×1×104 = -16＜0，∴此方程无实数根，∴不存在这样的x，使得此包装盒的容积为1560cm³.

答案： 5.解析　
(1)由题图得，包装盒的长为$\frac{40 - 2x}{2}=(20 - x)cm$，高为x cm，宽为15 cm，
∵此包装盒的容积为1500cm³，
∴15x(20 - x)=1500，解得x₁ = x₂ = 10，
∴x的值为10.
(2)[解法一]利用二次函数的性质解答:不存在.理由:设该包装盒的容积为y cm³，依题意得y = (20 - x)×15x=-15(x - 10)² + 1500.
∵-15＜0，
∴当x = 10时，此包装盒的容积最大，为1500cm³，
∴不存在这样的x，使得此包装盒的容积为1560cm³.
[解法二]利用一元二次方程根的判别式解答:不存在.理由:假设存在这样的x，则15x(20 - x)=1560，整理得x² - 20x + 104 = 0.
∵Δ = (-20)² - 4×1×104 = -16＜0，
∴此方程无实数根，
∴不存在这样的x，使得此包装盒的容积为1560cm³.