《2025年5年中考3年模拟九年级数学上册人教版》

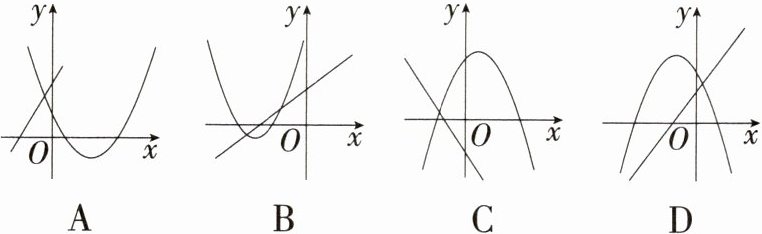
1. [2025山东德州德城期中]函数$y = ax + b(a \neq 0)与y = ax^{2}+bx + c(a \neq 0)$在同一平面直角坐标系中的图象可能是 (B)

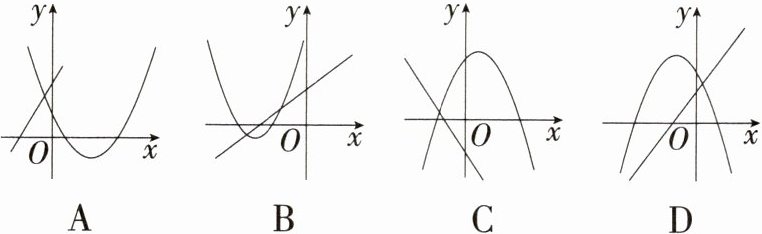
答案： B A. 由抛物线可知 $ a ＞ 0 $，$ b ＜ 0 $，由直线可知 $ a ＞ 0 $，$ b ＞ 0 $，矛盾，故本选项错误；B. 由抛物线可知 $ a ＞ 0 $，$ b ＞ 0 $，由直线可知 $ a ＞ 0 $，$ b ＞ 0 $，故本选项正确；C. 由抛物线可知 $ a ＜ 0 $，$ b ＞ 0 $，由直线可知 $ a ＜ 0 $，$ b ＜ 0 $，矛盾，故本选项错误；D. 由抛物线可知 $ a ＜ 0 $，$ b ＜ 0 $，由直线可知 $ a ＞ 0 $，$ b ＞ 0 $，矛盾，故本选项错误. 故选 B.

2. 在同一平面直角坐标系中,一次函数$y = cx + a与二次函数y = ax^{2}+bx + c$的图象可能是 (C)

答案： C A 项，由抛物线得 $ a ＜ 0 $，$ c ＞ 0 $，由直线得 $ c ＜ 0 $，$ a ＜ 0 $，矛盾；B 项，由抛物线得 $ a ＜ 0 $，$ c ＜ 0 $，由直线得 $ c ＞ 0 $，$ a ＞ 0 $，矛盾；C 项，由抛物线得 $ a ＞ 0 $，$ c ＜ 0 $，由直线得 $ c ＜ 0 $，$ a ＞ 0 $，符合题意；D 项，由抛物线得 $ a ＞ 0 $，$ c ＞ 0 $，由直线得 $ c ＞ 0 $，$ a ＜ 0 $，矛盾. 故选 C.

3. [2024山东泰安中考]如图所示的是二次函数$y = ax^{2}+bx + c(a \neq 0)$的部分图象,该函数图象的对称轴是直线$x = 1$,图象与$y$轴交点的纵坐标是2.则下列结论:①$2a + b = 0$;②方程$ax^{2}+bx + c = 0$一定有一个根在-2和-1之间;③方程$ax^{2}+bx + c - \frac{3}{2} = 0$一定有两个不相等的实数根;④$b - a ＜ 2$.其中正确结论的个数是 (B)

答案： B
∵ 抛物线的对称轴为直线 $ x = 1 $，
∴ $ -\frac{b}{2a} = 1 $，
∴ $ b = -2a $，
∴ $ 2a + b = 0 $，故①正确；
∵ 抛物线 $ y = ax^2 + bx + c $ 与 $ x $ 轴的一个交点在 $ (2, 0) $ 和 $ (3, 0) $ 之间，对称轴为直线 $ x = 1 $，
∴ 抛物线与 $ x $ 轴的另一个交点在 $ (-1, 0) $ 和 $ (0, 0) $ 之间，
∴ 方程 $ ax^2 + bx + c = 0 $ 一定有一个根在 $ -1 $ 和 $ 0 $ 之间，故②错误；
∵ 抛物线 $ y = ax^2 + bx + c $ 与直线 $ y = \frac{3}{2} $ 有两个交点，
∴ 方程 $ ax^2 + bx + c - \frac{3}{2} = 0 $ 一定有两个不相等的实数根，故③正确；
∵ 抛物线与 $ x $ 轴的一个交点在 $ (-1, 0) $ 和 $ (0, 0) $ 之间，
∴ 当 $ x = -1 $ 时，$ y = a - b + c ＜ 0 $，
∵ 图象与 $ y $ 轴交点的纵坐标是 $ 2 $，
∴ $ c = 2 $，
∴ $ a - b + 2 ＜ 0 $，
∴ $ b - a ＞ 2 $，故④错误. 故选 B.

4. [2024黑龙江绥化中考]二次函数$y = ax^{2}+bx + c(a \neq 0)$的部分图象如图所示,对称轴为直线$x = -1$,则下列结论:①$\frac{b}{c} ＞ 0$;②$am^{2}+bm \leq a - b$(m为任意实数);③$3a + c ＜ 1$;④若$M(x_{1},y),N(x_{2},y)$是抛物线上不同的两个点,则$x_{1}+x_{2} \leq -3$.其中正确的结论有 (B)
A.1个 B.2个 C.3个 D.4个

答案： B 由题图得抛物线开口向下，
∴ $ a ＜ 0 $，
∵ 抛物线的对称轴是直线 $ x = -\frac{b}{2a} = -1 $，
∴ $ b = 2a ＜ 0 $.
∵ 抛物线交 $ y $ 轴于正半轴，
∴ 当 $ x = 0 $ 时，$ y = c ＞ 0 $，
∴ $ \frac{b}{c} ＜ 0 $，故①错误. 由题意得，当 $ x = -1 $ 时，$ y $ 取最大值，为 $ a - b + c $，
∴ 对于抛物线上任意的点对应的函数值 $ y ≤ a - b + c $. 对于任意实数 $ m $，当 $ x = m $ 时，$ y = am^2 + bm + c ≤ a - b + c $，
∴ $ am^2 + bm ≤ a - b $，故②正确. 由图象可得，当 $ x = 1 $ 时，$ y = a + b + c ＜ 0 $，又
∵ $ b = 2a $，
∴ $ 3a + c ＜ 0 ＜ 1 $，故③正确.
∵ 点 $ M $，$ N $ 的纵坐标相等，
∴ 点 $ M $，$ N $ 关于直线 $ x = -1 $ 对称，
∴ $ x_1 + x_2 = -2 ＞ -3 $，故④错误. 综上，正确的结论有②③，共 2 个. 故选 B.

5. 如图所示的是二次函数$y = ax^{2}+bx + c$的部分图象,则不等式$ax^{2}+bx + c ＜ 0$的解集是 (C)
A.$x ＜ -1$ B.$x ＞ 5$ C.$x ＜ -1或x ＞ 5$ D.$-1 ＜ x ＜ 5$

答案： C 由题图可知，对称轴为直线 $ x = 2 $，
∵ 抛物线与 $ x $ 轴的一个交点坐标为 $ (5, 0) $，
∴ 抛物线与 $ x $ 轴的另一个交点坐标为 $ (-1, 0) $，又
∵ 抛物线开口向下，
∴ 不等式 $ ax^2 + bx + c ＜ 0 $ 的解集是 $ x ＜ -1 $ 或 $ x ＞ 5 $. 故选 C.

6. 如图,直线$y_{1} = kx + m与二次函数y_{2} = ax^{2}+bx + c(a ＞ 0)的图象交于点A(-2,3)和点B(2,-1)$,若$y_{2} ＜ y_{1} ＜ 0$,则$x$的取值范围是1＜x＜2.

答案： 答案 $ 1 ＜ x ＜ 2 $
解析 将 $ (-2, 3) $，$ (2, -1) $ 代入 $ y_1 = kx + m $ 得 $ \begin{cases} 3 = -2k + m \\ -1 = 2k + m \end{cases} $，解得 $ \begin{cases} k = -1 \\ m = 1 \end{cases} $，
∴ $ y_1 = -x + 1 $，令 $ y_1 = 0 $，则 $ -x + 1 = 0 $，解得 $ x = 1 $，
∴ 直线 $ y_1 $ 与 $ x $ 轴交点的坐标为 $ (1, 0) $，
∴ 由图象可知 $ y_2 ＜ y_1 ＜ 0 $ 时，$ 1 ＜ x ＜ 2 $.

7. 如图,已知抛物线经过$(-2,-3)和(3,-3)$两点,如果点$(1,y_{1})与(2,y_{2})$在此抛物线上,那么$y_{1}$＞$y_{2}$.(填“＞”“＜”或“=”)

答案： 答案 $ ＞ $
解析
∵ 抛物线经过 $ (-2, -3) $ 和 $ (3, -3) $ 两点，
∴ 抛物线的对称轴为直线 $ x = \frac{-2 + 3}{2} = \frac{1}{2} $，
∵ 抛物线的开口向下，$ \left| 1 - \frac{1}{2} \right| ＜ \left| 2 - \frac{1}{2} \right| $，
∴ $ y_1 ＞ y_2 $.

8. [2024浙江台州温岭期中]二次函数$y = x^{2}+bx + c$的图象如图所示,若其图象上有三点$A(-3,y_{1})$,$B(0,y_{2})$,$C(2,y_{3})$,则$y_{1},y_{2},y_{3}$的大小关系是$ y_3 ＞ y_2 ＞ y_1 $.

答案： 答案 $ y_3 ＞ y_2 ＞ y_1 $
解析 由题图可得，抛物线的对称轴为直线 $ x = -2 $，
∵ 抛物线开口向上，
∴ 抛物线上的点离对称轴越远，函数值越大，又
∵ $ | -3 - (-2) | ＜ | 0 - (-2) | ＜ | 2 - (-2) | $，
∴ $ y_3 ＞ y_2 ＞ y_1 $.