《2025年5年中考3年模拟九年级数学上册人教版》

10.学科易错题「2025 四川德阳月考,★☆」对于二次函数$y= x^{2}$,在$-1≤x≤2$的范围内的最大值和最小值分别为 (C)
A.最大值为 4,最小值为 1
B.最大值为 2,最小值为-1
C.最大值为 4,最小值为 0
D.最大值为 1,最小值为 0

答案： C
∵ y = x²，
∴ 二次函数图象的对称轴为直线 x = 0，且开口向上，
∴ 在 -1 ≤ x ≤ 2 的范围内，y 随 x 的增大先减小后增大，故当 x = 0 时，函数有最小值，为 0，当 x = 2 时，函数有最大值，为 4。故选 C。
易错点：易出现直接把两个临界值代入求出最大值和最小值的错误情况。

11.「2025 广东江门江海月考,★☆」已知$a≠0$,在同一直角坐标系中,函数$y= ax与y= ax^{2}$的图象有可能是 (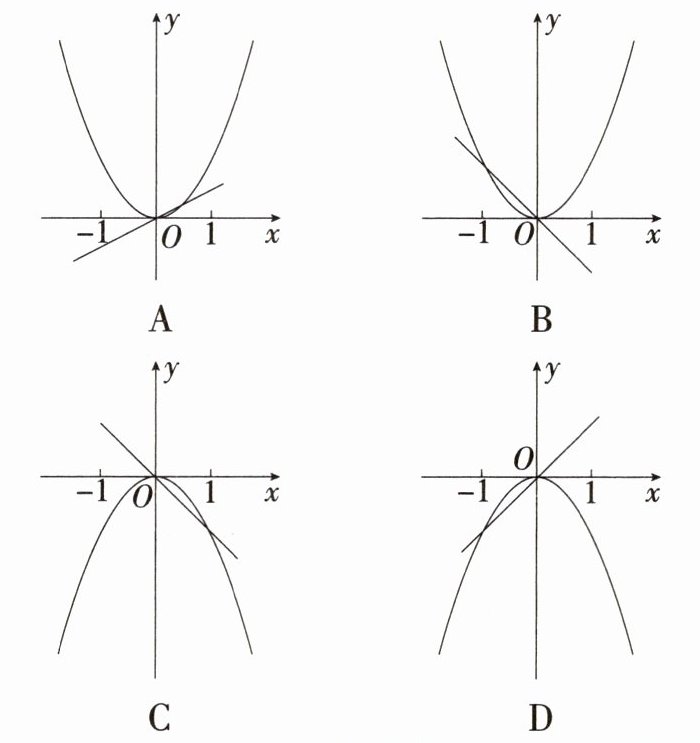C)
.

答案： C 当 a ＞ 0 时，函数 y = ax 的图象经过第一、三象限，函数 y = ax² 的图象开口向上，且两函数图象都经过点 (1, a)，无选项符合；当 a ＜ 0 时，函数 y = ax 的图象经过第二、四象限，函数 y = ax² 的图象开口向下，且两函数图象都经过点 (1, a)，选项 C 符合。故选 C。

12.「2025 北京房山期中,★☆」已知点$A(-1,3),B(3,3)$,若抛物线$y= ax^{2}$与线段 AB 只有一个公共点,则 a 的取值范围是 ( )
A.$0\lt a≤\frac {1}{3}$
B.$0\lt a＜3$
C.$\frac {1}{3}\lt a＜3$
D.$\frac {1}{3}≤a＜3$

答案：
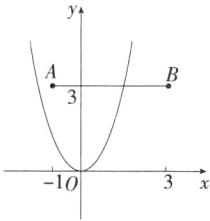
D 当 a ＜ 0 时，抛物线开口向下，此时抛物线与线段 AB 没有交点，不合题意；当 a ＞ 0 时，若抛物线 y = ax² 与线段 AB 只有一个公共点，则大致图象如图所示，
∴ 当 x = 3 时，y ≥ 3；当 x = -1 时，y ＜ 3，即 {9a ≥ 3，a ＜ 3}，解得 1/3 ≤ a ＜ 3。故选 D。

13.「★☆」如图,正方形四个顶点的坐标依次为$(1,1),(3,1),(3,3),(1,3)$.若抛物线$y= ax^{2}$与正方形有公共点,则实数 a 的取值范围是 (A)

A.$\frac {1}{9}≤a≤3$
B.$\frac {1}{9}≤a≤1$
C.$\frac {1}{3}≤a≤3$
D.$\frac {1}{3}≤a≤1$

答案： A
∵ |a| 越大，抛物线 y = ax² 开口越小。由题图知，a ＞ 0，易知抛物线与正方形有公共点的临界点分别为 (3, 1)、(1, 3)。
当抛物线经过点 (1, 3) 时，a = 3；
当抛物线经过点 (3, 1) 时，a = 1/9。
∴ 当抛物线 y = ax² 与正方形有公共点时，1/9 ≤ a ≤ 3。故选 A。

14.新推理能力新动态探究题 如图,点 P 为抛物线$y= \frac {1}{4}x^{2}$上一动点.若直线 l 经过 y 轴上一点 N,且平行于 x 轴,点 N 的坐标为$(0,-1)$,过点 P 作$PM⊥$直线 l 于 M.
(1)如图 1,在抛物线的对称轴上是否存在一定点 F,使得$PM= PF$恒成立? 若存在,求出点 F 的坐标;若不存在,请说明理由.
(2)如图 2,若点 Q 的坐标为$(1,5)$,求$QP+PF$的最小值.

答案：
解析
(1) 存在。设 P(t, 1/4t²)，F(0, h)，
如图，过点 P 作 PG⊥y 轴于点 G，则 G(0, 1/4t²)，
∴ FG = 1/4t² - h，PG = t，PM = 1/4t² - (-1) = 1/4t² + 1，
若 PM = PF，则 PM² = PF² = PG² + FG²，
∴ (1/4t² + 1)² = t² + (1/4t² - h)²，化简得 1/2t² - 1/2t²h + h² - 1 = 0，
∴ 1/2t²(1 - h) + (h + 1)(h - 1) = 0，
即 (h - 1)(h + 1 - 1/2t²) = 0，
因为点 P 为动点，所以当 h = 1 时，t 取任何值上述等式恒成立，
∴ 存在定点 F(0, 1)，使 PM = PF 恒成立。

(2)
∵ PM = PF，
∴ QP + PF = QP + PM。
当 Q，P，M 三点共线时，QP + PF 取最小值。
∵ Q(1, 5)，点 M 的纵坐标为 -1，
∴ 当 QM⊥直线 l 时，QP + PF 的值最小，为 5 - (-1) = 6。