第110页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
- 第164页
- 第165页
- 第166页
- 第167页
- 第168页
- 第169页
- 第170页
- 第171页
- 第172页
- 第173页
- 第174页
- 第175页
- 第176页
- 第177页
- 第178页
- 第179页
- 第180页
- 第181页
- 第182页
- 第183页
- 第184页
- 第185页
- 第186页
- 第187页
- 第188页
- 第189页
- 第190页
- 第191页
- 第192页
- 第193页
- 第194页
- 第195页
- 第196页
- 第197页
- 第198页
- 第199页
- 第200页
- 第201页
- 第202页
- 第203页
- 第204页
- 第205页
7. 跨学科(2024内江)如图所示的电路中,当随机闭合开关$S_{1}$,$S_{2}$,$S_{3}$中的两个时,灯泡能发光的概率为(
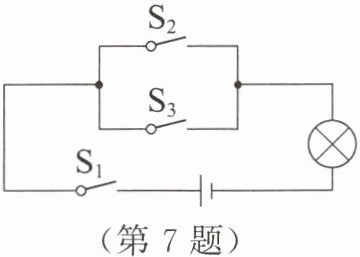
A. $\frac{2}{3}$
B. $\frac{1}{2}$
C. $\frac{1}{3}$
D. $\frac{1}{6}$
A
)
A. $\frac{2}{3}$
B. $\frac{1}{2}$
C. $\frac{1}{3}$
D. $\frac{1}{6}$
答案:
A
8. (2024武汉)经过某十字路口的汽车,可能直行,也可能向左转或向右转,这三种可能性大小相同.若两辆汽车经过这个十字路口,则至少一辆车向右转的概率是(
A. $\frac{1}{9}$
B. $\frac{1}{3}$
C. $\frac{4}{9}$
D. $\frac{5}{9}$
D
)A. $\frac{1}{9}$
B. $\frac{1}{3}$
C. $\frac{4}{9}$
D. $\frac{5}{9}$
答案:
D
9. (2024南充改编)某研学基地开设有A,B,C,D四类研学项目.为了解学生对四类研学项目的喜爱情况,随机抽取部分参加完研学项目的学生进行调查统计(每名学生必须选择一项,并且只能选择一项),并将调查结果绘制成两幅不完整的统计图,如图所示.
根据图中信息,解答下列问题:
(1)参加调查统计的学生中喜爱B类研学项目的有
(2)从参加调查统计喜爱D类研学项目的4名学生(2名男生和2名女生)中,随机选取2人接受访谈,求恰好选中1名男生和1名女生的概率为
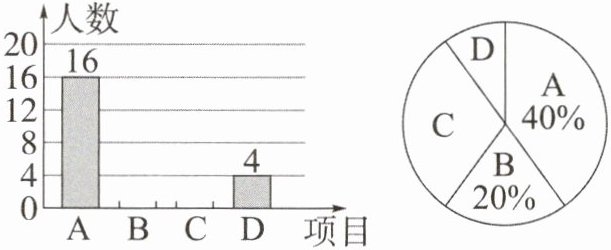
根据图中信息,解答下列问题:
(1)参加调查统计的学生中喜爱B类研学项目的有
8
人?在扇形统计图中,求C类研学项目所在扇形的圆心角的度数为108°
.(2)从参加调查统计喜爱D类研学项目的4名学生(2名男生和2名女生)中,随机选取2人接受访谈,求恰好选中1名男生和1名女生的概率为
$\frac{2}{3}$
.
答案:
(1) 喜爱B类研学项目的有8人,C类研学项目所在扇形的圆心角的度数为$108^{\circ}$
(2) $\frac{2}{3}$
(1) 喜爱B类研学项目的有8人,C类研学项目所在扇形的圆心角的度数为$108^{\circ}$
(2) $\frac{2}{3}$
10. (2023福建)为促进消费,助力经济发展,某商场决定“让利酬宾”,于“五一”期间举办了抽奖促销活动.活动规定:凡在商场消费一定金额的顾客,均可获得一次抽奖机会.抽奖方案如下:从装有大小、质地完全相同的1个红球及编号为①②③的3个黄球的袋中,随机摸出1个球,若摸得红球,则中奖,可获得奖品;若摸得黄球,则不中奖.同时,还允许未中奖的顾客将其摸得的球放回袋中,并再往袋中加入1个红球或黄球(它们的大小、质地与袋中的4个球完全相同),然后从中随机摸出1个球,记下颜色后不放回,再从中随机摸出1个球,若摸得的两球的颜色相同,则该顾客可获得精美礼品一份.现已知某顾客获得抽奖机会.
(1)求该顾客首次摸球中奖的概率.
(2)假如该顾客首次摸球未中奖,为了有更大机会获得精美礼品,他应往袋中加入哪种颜色的球?说明你的理由.
(1)求该顾客首次摸球中奖的概率.
(2)假如该顾客首次摸球未中奖,为了有更大机会获得精美礼品,他应往袋中加入哪种颜色的球?说明你的理由.
答案:
解:
(1) 顾客首次摸球的所有可能结果为红,黄①,黄②,黄③,共4种等可能的结果.
记“首次摸得红球”为事件A,则事件A发生的结果只有1种,
∴$P(A)=\frac{1}{4}$,即该顾客首次摸球中奖的概率为$\frac{1}{4}$.
(2) 他应往袋中加入黄球. 理由: 记往袋中加入的球为“新”,摸得的两球所有可能的结果列表如下:
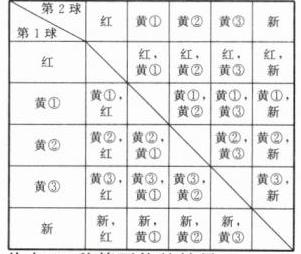
共有20种等可能的结果.
(ⅰ) 若往袋中加入的是红球,两球颜色相同的结果共有8种,此时该顾客获得精美礼品的概率$P_{1}=\frac{8}{20}=\frac{2}{5}$.
(ⅱ) 若往袋中加入的是黄球,两球颜色相同的结果共有12种,此时该顾客获得精美礼品的概率$P_{2}=\frac{12}{20}=\frac{3}{5}$.
∵$\frac{2}{5}<\frac{3}{5}$,
∴$P_{1}<P_{2}$.
∴他应往袋中加入黄球.
解:
(1) 顾客首次摸球的所有可能结果为红,黄①,黄②,黄③,共4种等可能的结果.
记“首次摸得红球”为事件A,则事件A发生的结果只有1种,
∴$P(A)=\frac{1}{4}$,即该顾客首次摸球中奖的概率为$\frac{1}{4}$.
(2) 他应往袋中加入黄球. 理由: 记往袋中加入的球为“新”,摸得的两球所有可能的结果列表如下:

共有20种等可能的结果.
(ⅰ) 若往袋中加入的是红球,两球颜色相同的结果共有8种,此时该顾客获得精美礼品的概率$P_{1}=\frac{8}{20}=\frac{2}{5}$.
(ⅱ) 若往袋中加入的是黄球,两球颜色相同的结果共有12种,此时该顾客获得精美礼品的概率$P_{2}=\frac{12}{20}=\frac{3}{5}$.
∵$\frac{2}{5}<\frac{3}{5}$,
∴$P_{1}<P_{2}$.
∴他应往袋中加入黄球.
查看更多完整答案,请扫码查看


