《2025年通城学典课时作业本八年级数学下册华师大版》

7.如图,过四边形ABCD的顶点A、C、B、D分别作BD、AC的平行线，围成四边形EFGH.如果要判定四边形EFGH是菱形,那么四边形ABCD必定是　　　　　　　　　　　(　　　)
　
A.菱形
　
B.平行四边形
　
C.一组对边平行的四边形
　
D.对角线相等的四边形
　　　　

答案： D

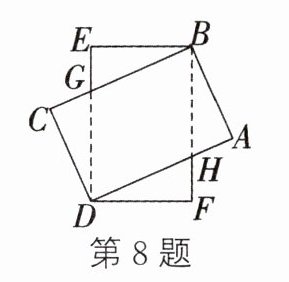
8.(2024.衡阳期末)有两个全等矩形纸条,长与宽分别为18和12,按如图所示的方式交叉叠放在一起，则重合部分构成的四边形
BGDH的周长为__________.

答案： 52　解析:由题意,得∠EBF=∠CBA=90°,AB=BE=12,AD//BC,BF//DE,AD=18,
∴四边形BGDH是平行四边形.
∴S平行四边形BGDH=BG·AB=BH·BE.
∴BG=BH.
∴四边形BGDH是菱形.
∴BH=DH.
设BH=DH=x,则AH=18−x.
在Rt△ABH中，由勾股定理,得AB²+AH²=BH²,即12²+(18 - x)²=x²,解得x=13.
∴BH=13.
∴四边形BGDH的周长 = 4BH=52.

9.如图,在▱ABCD中,∠BAD的平分线AE 交BC于点E,∠ABC的平分线BF交AD 于点F,AE与BF相交于点O,连结EF.
　(1)求证:四边形ABEF是菱形;
　(2)若AE=6,BF=8,CE=2,求ABCD 的面积.
　　　　　　　　　　　　　

答案：

(1)
∵四边形ABCD是平行四边形，
∴AD//BC.
∴∠DAE=∠AEB,AF//BE.
∵AE平分∠BAD，
∴∠DAE=∠BAE.
∴∠BAE=∠AEB.
∴AB=BE.
同理，可得AB=AF.
∴AF=BE.
∴四边形ABEF是平行四边形.
∵AB=AF,
∴四边形ABEF是菱形
(2)如图，过点A作AG⊥BC于点G.
∵四边形ABEF是菱形,AE=6,BF=8,
∴AE⊥BF,OE=$\frac{1}{2}$AE=3,OB=$\frac{1}{2}$BF=4.
∴∠BOE=90°.
在Rt△BOE中，由勾股定理，得BE = $\sqrt{OE²+OB²}$ = $\sqrt{3²+4²}$ = 5.
∵S菱形ABEF=$\frac{1}{2}$AE·BF=BE·AG,即$\frac{1}{2}$×6×8=5AG,
∴AG=$\frac{24}{5}$.
∴S平行四边形ABCD=BC·AG=(BE+CE)·AG=$\frac{168}{5}$

10.如图①,在矩形纸片ABCD中,AB=3cm,
AD=5cm,折叠纸片使点B落在边AD上的点E处,折痕为PQ.过点E作EF//AB 交PQ于点F,连结BF.
　　(1)求证:四边形BFEP是菱形.
　　(2)当点E在边AD上移动时,折痕的端点P、Q也随之移动.如图②,当点Q与点C 重合时,求菱形BFEP的面积.
　　　

答案：
(1)由折叠,可知PB=PE,BF=EF,∠BPF=∠EPF.
又
∵EF//AB,
∴∠BPF=∠EFP.
∴∠EPF=∠EFP.
∴PE=EF.
∴PB=BF=EF=PE.
∴四边形BFEP是菱形
(2)
∵四边形ABCD是矩形，
∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°.
由折叠,知CE=BC=5cm,PE=PB.
在Rt△CDE中,由勾股定理,得DE = $\sqrt{CE²−CD²}$ = $\sqrt{5²−3²}$ = 4(cm).
∴AE=AD−DE=5−4=1(cm).
设PE=PB=xcm.
∴AP=AB−PB=(3−x)cm.
在Rt△APE中,由勾股定理,得PE²=AE²+AP²,即x²=1²+(3−x)²,解得x = $\frac{5}{3}$.
∴PB=$\frac{5}{3}$cm.
∴S菱形BFEP=PB·AE=$\frac{5}{3}$×1=$\frac{5}{3}$(cm²)