《2025年通城学典课时作业本八年级数学下册华师大版》

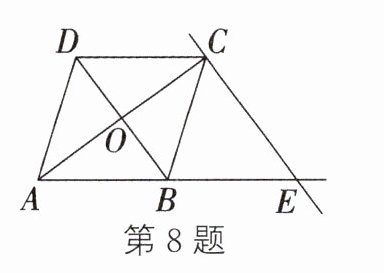
8.如图,在菱形ABCD中,对角线AC、BD相交于点O,过点C作CE//BD,交AB的延长线于点E.下列结论中,不一定正确的是(　　　)


A.OB = $\frac{1}{2}$CE
B.∠ACE = 90°
C.BC = $\frac{1}{2}$AE
D.BE = CE

答案： D

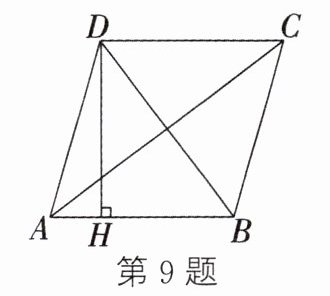
9.(2024.新乡辉县期末)如图,四边形ABCD是菱形,AC = 8,BD = 6,DH⊥AB于点H,则DH的长为__________.

答案： $\frac{24}{5}$ 解析：设对角线AC与BD相交于点O.
∵四边形ABCD是菱形，AC = 8，BD = 6，
∴AC⊥BD，OA = $\frac{1}{2}$AC = 4，OB = $\frac{1}{2}$BD = 3.
∴∠AOB = 90°.在Rt△AOB中，由勾股定理，得AB = $\sqrt{OA^{2}+OB^{2}}$ = 5.
∵S菱形ABCD = $\frac{1}{2}$AC·BD = 24，DH⊥AB，
∴S菱形ABCD = DH·AB = 24.
∴DH = $\frac{24}{5}$.

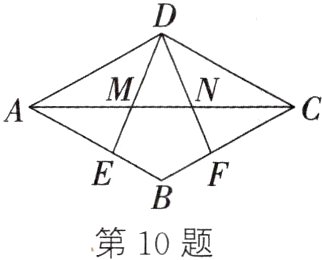
10.如图,在菱形ABCD中,点E、F分别在边AB、BC上,BE = BF,DE、DF分别与AC相交于点M、N.求证:
(1)△ADE≌△CDF;
(2)ME = NF.

答案：
(1)
∵四边形ABCD是菱形，
∴DA = DC，∠DAE = ∠DCF，AB = BC.
∵BE = BF，
∴易得AE = CF.在△ADE和△CDF中，$\begin{cases}DA = DC\\∠DAE = ∠DCF\\AE = CF\end{cases}$，
∴△ADE≌△CDF.
(2)由
(1)，知△ADE≌△CDF.
∴∠ADE = ∠CDF，DE = DF.
∵DA = DC，
∴∠DAM = ∠DCN.
∴易得∠DMA = ∠DNC.
∵∠DMN = 180° - ∠DMA，∠DNM = 180° - ∠DNC，
∴∠DMN = ∠DNM.
∴DM = DN.
∴DE - DM = DF - DN，即ME = NF.

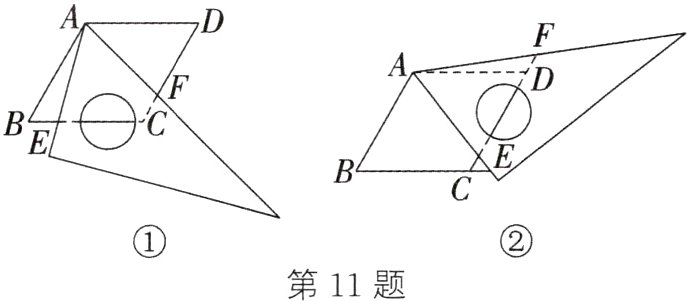
11.如图,在菱形ABCD中,∠B = 60°,把一块含60°角的三角尺与这个菱形叠合，使三角尺60°角的顶点与点A重合，将三角尺绕点A按逆时针方向旋转.
(1)如图①,三角尺的两边分别与菱形的两边BC、CD相交于点E、F.求证:CE + CF = AB.
(2)如图②,三角尺的两边分别与菱形的两边BC、CD的延长线相交于点E、F.写出此时CE、CF、AB之间的数量关系,并说明理由.

答案：
(1)如图①，连结AC.
∵四边形ABCD是菱形，
∴AB = BC = CD = DA，∠B = ∠D = 60°.
∴△ABC、△ACD都是等边三角形.
∴AB = AC，∠BAC = ∠ACD = ∠B = 60°.
∵∠EAF = 60°，
∴∠BAC = ∠EAF.
∴∠BAC - ∠EAC = ∠EAF - ∠EAC，即∠BAE = ∠CAF.在△BAE和△CAF中，$\begin{cases}∠BAE = ∠CAF\\AB = AC\\∠B = ∠ACF\end{cases}$，
∴△BAE≌△CAF.
∴BE = CF.
∴CE + CF = CE + BE = BC，即CE + CF = AB.
(2)CF - CE = AB.理由：如图②，连结AC.
∵四边形ABCD是菱形，
∴∠B = ∠ADC = 60°，AB = BC = CD = DA.
∴△ABC、△ACD都是等边三角形.
∴AD = AC，∠ACB = ∠ADC = ∠CAD = 60°.
∴易得∠ACE = ∠ADF = 120°.
∵∠EAF = 60°，
∴∠CAD = ∠EAF.
∴易得∠CAE = ∠DAF.在△ACE和△ADF中，$\begin{cases}∠CAE = ∠DAF\\AC = AD\\∠ACE = ∠ADF\end{cases}$，
∴△ACE≌△ADF.
∴CE = DF.
∴CF - CE = CF - DF = CD，即CF - CE = AB.