《2025年通城学典课时作业本八年级数学下册华师大版》

13.机器狗是一种模拟真实犬只形态和部分行为的机器装置,其最快移动速度(m/s)是载重后总质量m(kg)的反比例函数.已知一款机器狗载重后总质量为60kg时,它的最快移动速度为6m/s;当其载重后总质量为90kg时,它的最快移动速度为________m/s.

答案： 4

14.如图，一条垂直于x轴的直线分别交函数y = $\frac{10}{x}$(x＞0)与y = $\frac{6}{x}$(x＞0)的图象于点A、B,连结OA、OB,则△AOB的面积为________.

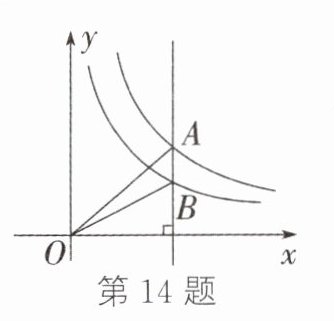
答案： 2

15.(2024.南阳桐柏期末)如图,一次函数y = kx + b(k≠0)的图象与反比例函数y = $\frac{1}{x}$的图象交于( - 1,m)、( - 5,n)两点,则不等式kx + b - $\frac{1}{x}$＞0的解集为________________.

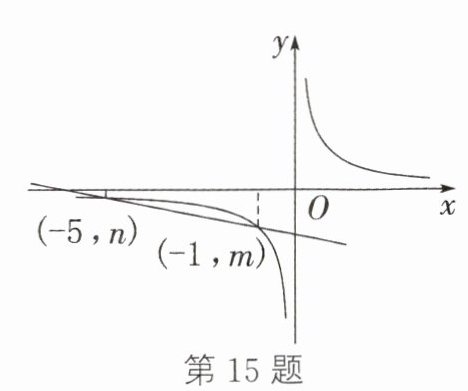
答案： x＜−5或−1＜x＜0。解析：由题图，可知当x＜−5和−1＜x＜0时，一次函数的图象在反比例函数的图象的上方，即kx + b＞$\frac{1}{x}$。所以不等式kx + b - $\frac{1}{x}$＞0的解集为x＜−5或−1＜x＜0。

16.(2024.长春二道模拟)输液管上有一个调节滴速的开关.对于不同的药物,不同体质的人输液速度不相同.下表记录了某次输液40min内5个时间点的剩余药液量,其中t(min)表示输液所用时间,y(mL)表示剩余药液量.

根据以上信息解决问题:
(1)研究发现剩余药液量y(mL)与输液所用时间t(min)之间存在函数关系,在平面直角坐标系中,描出上表中所对应的点,根据描出的点连线画出函数图象;
(2)结合表中数据,求y关于t的函数表达式;
(3)在这种输液速度下，由函数图象可知100mL药液需要________min输完.

答案：

(1)描点，连线，画出图象如图所示。
(2)设y关于t的函数表达式为y = kt + b(k≠0)，把(0,100)，(10,85)代入，得$\begin{cases}b = 100\\10k + b = 85\end{cases}$，解得$\begin{cases}k = -1.5\\b = 100\end{cases}$。所以y关于t的函数表达式为y = -1.5t + 100。
(3)$\frac{200}{3}$

17.如果点A(a + 1,b - 2)在第二象限,那么点B( - a,1 - b)在(　　)
A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： D

18.已知一次函数y = kx - m - 2x的图象与y轴的负半轴相交,且y随x的增大而减小,则下列结论正确的是(　　)
A.k＜2,m＞0
B.k＜2,m＜0
C.k＞2,m＞0
D.k＞2,m＜0

答案： A