《2025年通城学典课时作业本八年级数学下册华师大版》

1.(2024·衡阳段考)在同一平面直角坐标系中,函数y = -$\frac{a}{x}$与y = ax + 1(a ≠ 0)的图象可能是(　　)

答案： B

2.如图,直线y = kx + 1与双曲线y = $\frac{2}{x}$在第一象限内交于点P(1, t),与x轴、y轴分别交于点A、B,则下列结论错误的是(　　)


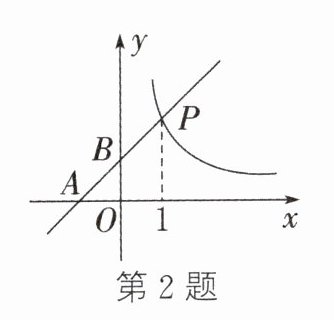
A.t = 2
B.△AOB是等腰直角三角形
C.k = 1
D.当x ＞ 1时，$\frac{2}{x}$ ＞ kx + 1

答案： D

3.函数y = x(x ≥ 0)和y = $\frac{4}{x}$(x ＞ 0)的图象如图所示.有下列结论:①两函数图象的交点A的坐标为(2, 2);②当x ＞ 2时,$\frac{4}{x}$ ＜ x;③直线x = 1分别与两函数图象相交于B、C两点,则S△OBC = $\frac{3}{2}$;④函数y = x(x ≥ 0)的值随x的增大而增大,函数y = $\frac{4}{x}$(x ＞ 0)的值随x的增大而减小.其中,正确的是________(填序号).

答案： ①③④

4.如图,在平面直角坐标系中,一次函数y = kx + b的图象与反比例函数y = $\frac{m}{x}$的图象相交于点A(-1, n)、B(2, 1).
(1)求一次函数、反比例函数的表达式;
(2)连结OA、OB,求△AOB的面积.

答案：

(1)
∵反比例函数y=$\frac{m}{x}$的图象经过点A(−1,n)、B(2,1),
∴$\frac{m}{2}$=1,
∴m=2,
∴反比例函数的表达式为y=$\frac{2}{x}$.把x = -1代入y=$\frac{2}{x}$，得n = -2,
∴A(−1,−2).
∵一次函数y=kx+b的图象经过点A(−1,−2)、B(2,1),
∴$\begin{cases}-k + b = -2 \\2k + b = 1 \end{cases}$，解得$\begin{cases}k = 1 \\b = -1 \end{cases}$，
∴一次函数的表达式为y=x−1.
(2)如图，设一次函数的图象与x轴的交点为C,在函数y=x−1中,当y=0时,x=1,
∴C(1,0),即OC=1.
∴$S_{\triangle AOB}=S_{\triangle BOC}+S_{\triangle AOC}=\frac{1}{2}\times1\times1+\frac{1}{2}\times1\times2=\frac{3}{2}$

5.如图，一次函数的图象与反比例函数的图象交于点A(-1, 6)、B($\frac{3}{a}$, a - 3),与x轴交于点C,与y轴交于点D.
(1)求反比例函数、一次函数的表达式.
(2)已知点M在x轴上,连结OA、OB.若S△AOM = S△AOB,求点M的坐标.

答案：
(1)由题意，设反比例函数的表达式为y=$\frac{n}{x}$(n≠0),一次函数的表达式为y=kx+b(k≠0).
∵点A(−1,6)在反比例函数的图象上，
∴$\frac{n}{-1}$=6,
∴n = -6,
∴反比例函数的表达式为y=$-\frac{6}{x}$.
∵点B($\frac{3}{a}$,a - 3)在反比例函数的图象上,
∴$\frac{3}{a}(a - 3)= - 6$,
去分母得$3(a - 3)= - 6a$，
$3a - 9 = - 6a$，
$3a + 6a = 9$，
$9a = 9$，
解得a = 1,
∴B(3,−2).
∵点A(−1,6)、B(3,−2)在一次函数y=kx+b(k≠0)的图象上，
∴$\begin{cases}-k + b = 6 \\3k + b = -2 \end{cases}$，解得$\begin{cases}k = -2 \\b = 4 \end{cases}$，
∴一次函数的表达式为y = -2x + 4.
(2)设点M的坐标为(m,0).
对于y = -2x + 4,令y = 0,得 -2x + 4 = 0,解得x = 2,
∴C(2,0),
∴OC = 2.
∴$S_{\triangle AOB}=S_{\triangle AOC}+S_{\triangle BOC}=\frac{1}{2}OC\cdot|y_A|+\frac{1}{2}OC\cdot|y_B|=\frac{1}{2}\times2\times6+\frac{1}{2}\times2\times2=6 + 2 = 8$.
∵$S_{\triangle AOM}=\frac{1}{2}OM\cdot|y_A|=\frac{1}{2}|m|\times6 = 3|m|$，$S_{\triangle AOM}=S_{\triangle AOB}$，
∴3|m| = 8,
∴m = ±$\frac{8}{3}$,
∴点M的坐标为($\frac{8}{3}$,0)或(−$\frac{8}{3}$,0).

6.如图,正比例函数y = $\frac{1}{2}$x的图象与反比例函数y = $\frac{k}{x}$(k ≠ 0, x ＞ 0)的图象交于点A,过点A作x轴的垂线，垂足为M,△OAM的面积为1,B为该反比例函数图象上的一点(点B不与点A重合),且点B的横坐标为1.若点P在x轴上,则当PA + PB的值最小时,点P的坐标为________.

答案： ($\frac{5}{3}$,0) 解析:设点A的坐标为(a,b),则b = $\frac{k}{a}$,
∴ab = k.
∵$S_{\triangle OAM}=1$,
∴$\frac{1}{2}ab = 1$,即$\frac{1}{2}k = 1$,
∴k = 2,
∴反比例函数的表达式为y = $\frac{2}{x}$.
当x = 1时,y = 2,
∴B(1,2).
联立方程组$\begin{cases}y = \frac{2}{x} \\y = \frac{1}{2}x \end{cases}$，
将$y = \frac{1}{2}x$代入$y = \frac{2}{x}$得$\frac{1}{2}x=\frac{2}{x}$，
$x^2 = 4$，
解得$\begin{cases}x = 2 \\y = 1 \end{cases}$或$\begin{cases}x = -2 \\y = -1 \end{cases}$(不合题意，舍去).
∴A(2,1).
设点A关于x轴的对称点为C,则点C的坐标为(2,−1).
连结BC，交x轴于点P,易知此时PA + PB的值最小.
设直线BC对应的函数表达式为y = mx + n(m≠0).
将B(1,2)、C(2,−1)代入,得$\begin{cases}m + n = 2 \\2m + n = -1 \end{cases}$，解得$\begin{cases}m = -3 \\n = 5 \end{cases}$，
∴直线BC对应的函数表达式为y = -3x + 5.
当y = 0时,x = $\frac{5}{3}$,
∴点P的坐标为($\frac{5}{3}$,0).

7.为加强生态文明建设,某市环保局对一企业所排污水进行检测，结果显示所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1mg/L.环保局要求该企业立即整改,在15天内(含第15天)排污达标.在整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示.其中,线段AC表示前3天的变化规律，第3天所排污水中硫化物的浓度降为4.5mg/L.从第3天起,所排污水中硫化物的浓度y(mg/L)与时间x(天)满足下表中的关系.

(1)在整改过程中,求当0 ≤ x ＜ 3时,y与x 之间的函数表达式.
(2)在整改过程中,求当x ≥ 3时,y与x之间的函数表达式.
(3)该企业所排污水中硫化物的浓度能否在15天内达标？为什么？

答案：
(1)设线段AC所在直线对应的函数表达式为y = kx + b (k≠0).
将(0,12)、(3,4.5)代入，得$\begin{cases}b = 12 \\3k + b = 4.5 \end{cases}$，解得$\begin{cases}k = -2.5 \\b = 12 \end{cases}$，
∴y = -2.5x + 12(0≤x＜3).
(2)
∵3×4.5 = 5×2.7 = 6×2.25 = 9×1.5 = 13.5,
∴当x≥3时，y是x的反比例函数.
∴易得函数表达式为y = $\frac{13.5}{x}$(x≥3).
(3)能 当x = 15时,y = $\frac{13.5}{15}$ = 0.9.
∵0.9＜1,
∴该企业所排污水中硫化物的浓度能在15天内达标.

1.(2024.宜宾段考)一本笔记本的售价为6元.若小青买x本这样的笔记本共付y元,则x和6分别是(　　)
A.常量,变量
B.变量,常量
C.常量,常量
D.变量,变量

答案： B

2.匀速地向如图所示的空容器内注水,直到把容器注满.在注水过程中,容器内水面高度h随时间t变化的大致图象是(　　)

答案： C

3.(2024.汉中期末)如图所示的图象表示一辆汽车在某一条直线公路上的行驶过程中,离出发地的距离s(km)和行驶时间t(h)之间的函数关系.根据图中提供的信息，下列说法中,正确的是(　　)

A.汽车一共行驶了120km
B.汽车出发后前3h的平均速度为50km/h
C.汽车在整个行驶过程中停留了2h
D.汽车出发后3h至4.5h之间的平均速度为80km/h

答案： D