《2025年通城学典课时作业本八年级数学下册华师大版》

6. 小明参加100m短跑训练，2024年1 - 4月的训练成绩如下表：

体育老师夸奖小明是“田径天才”，请你预测小明5年（60个月）后100m短跑的成绩为（提示：目前100m短跑的世界纪录为9.58s）（ ）
A. 14.8s
B. 3.8s
C. 3s
D. 预测结果不可靠

答案： D

7. 如图所示为一种单肩包，其背带由双层部分、单层部分和调节扣构成。小文购买时，售货员演示通过调节扣加长或缩短单层部分的长度，可以使背带的长度（单层部分与双层部分长度的和，其中调节扣所占长度忽略不计）加长或缩短，设双层部分的长度为xcm，单层部分的长度为ycm。经测量，得到表中数据。

(1) 根据表中数据规律，求出y关于x的函数表达式；
(2) 按小文的身高和习惯，背带的长度调为130cm时为最佳背带长，请计算此时双层部分的长度；
(3) 设背带的长度为Lcm，求L的取值范围。

答案：
(1)由题表中的数据，可知x每增加6cm，y相应减少12cm，
∴y与x之间是一次函数的关系。设y关于x的函数表达式为y = kx + b(k ≠ 0)。将题表中两组较简单的对应数据(x = 2，y = 148；x = 8，y = 136)代入，得$\begin{cases}2k + b = 148 \\ 8k + b = 136 \end{cases}$，解得$\begin{cases}k = -2 \\ b = 152 \end{cases}$，
∴y关于x的函数表达式为y = -2x + 152。
(2)根据题意，得$\begin{cases}x + y = 130 \\ y = -2x + 152 \end{cases}$，解得$\begin{cases}x = 22 \\ y = 108 \end{cases}$，
∴此时双层部分的长度为22cm。
(3)在y = -2x + 152中，当x = 0时，y = 152；当y = 0时，x = 76。
∴背带的长度L的取值范围是76 ≤ L ≤ 152。

8. 汛期到来，下表记录了某水库20h内水位的变化情况，其中x(h)表示时间，y(m)表示水位。当x = 8时，达到警戒水位，开始开闸放水。

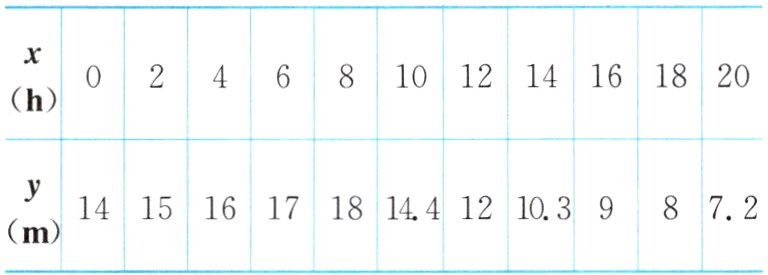
(1) 如图，在平面直角坐标系中，根据表格中的数据画出水位的变化图象，当水位高出16m时，x的取值范围是__________；
(2) 请分别求出开闸放水前和放水后最符合表中数据的函数表达式；
(3) 据估计，开闸放水后，水位的这种变化规律会持续一段时间，预测何时水位变为6m。

答案：

(1)画图象如图所示，4＜x＜9。
(2)观察图象，可知当0 ≤ x ≤ 8时，y与x之间的关系符合一次函数关系。设y = kx + b(k ≠ 0)。把(0，14)、(8，18)代入，得$\begin{cases}b = 14 \\ 8k + b = 18 \end{cases}$，解得$\begin{cases}k = \frac{1}{2} \\ b = 14 \end{cases}$，
∴y = $\frac{1}{2}$x + 14(0 ≤ x ≤ 8)。观察图象，可知当x＞8时，y与x之间的关系不是一次函数关系。通过观察数据，发现8×18 = 10×14.4 = 12×12 = 16×9 = 18×8 = 20×7.2 = 144。因此，开闸放水后y与x之间的关系符合反比例函数关系，其表达式为y = $\frac{144}{x}$(x＞8)。
(3)当y = 6时，6 = $\frac{144}{x}$，解得x = 24，即预测24h时水位变为6m。