《2025年通城学典课时作业本八年级数学下册华师大版》

7. 某快递公司每天的上午9:00~10:00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数关系如图所示.当两仓库的快件数量相同时，此刻的时间为(　　)


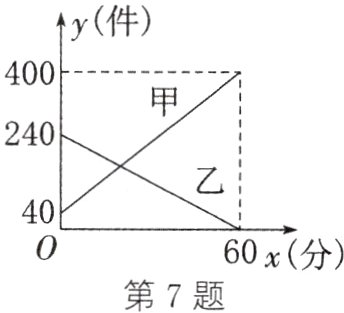
A. 9:15
B. 9:20
C. 9:25
D. 9:30

答案： B

8. 若直线y = -2x - 4与直线y = 4x + b的交点在第三象限，则b的取值范围是________.

答案： -4 ＜ b ＜ 8 解析:解方程组{y = -2x - 4, y = 4x + b}，得x = -$\frac{b + 4}{6}$，y = $\frac{b - 8}{3}$。
∴直线y = -2x - 4与直线y = 4x + b的交点坐标为(-$\frac{b + 4}{6}$, $\frac{b - 8}{3}$)。由题意，得{-$\frac{b + 4}{6}$ ＜ 0, $\frac{b - 8}{3}$ ＜ 0}，解得 -4 ＜ b ＜ 8。

9. 点A、B、C、D的坐标如图所示，求直线AB与直线CD的交点坐标.

答案： 设直线AB对应的函数表达式为y = kx + b(k ≠ 0)。将A(-3, 0)、B(0, 6)代入，得{-3k + b = 0, b = 6}，解得{k = 2, b = 6}。
∴直线AB对应的函数表达式为y = 2x + 6。同理，可得直线CD对应的函数表达式为y = -$\frac{1}{2}$x + 1。联立方程组{y = 2x + 6, y = -$\frac{1}{2}$x + 1}，解得{x = -2, y = 2}。
∴直线AB与直线CD的交点坐标为(-2, 2)。

10. 为响应绿色出行的号召，越来越多的市民选择租用共享单车出行.已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式，如图所示为两种支付方式支付的金额y(元)与骑行时间x(时)之间的函数图象.根据图象，解答下列问题:
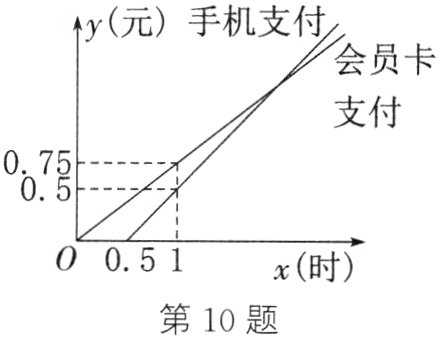
(1)求手机支付金额y(元)关于骑行时间x(时)的函数表达式.
(2)当骑行时间为多久时，两种支付方式支付的金额相同？
(3)如果李老师经常骑共享单车，且每次骑行约2.5小时，那么选择哪种支付方式比较合算？

答案：
(1)当0 ≤ x ＜ 0.5时，y = 0。当x ≥ 0.5时，设手机支付金额y(元)关于骑行时间x(时)的函数表达式为y = kx + b(k ≠ 0)。将(0.5, 0)、(1, 0.5)代入，得{0.5k + b = 0, k + b = 0.5}，解得{k = 1, b = -0.5}。
∴y = x - 0.5。
∴手机支付金额y(元)关于骑行时间x(时)的函数表达式为y = {0(0 ≤ x ＜ 0.5), x - 0.5(x ≥ 0.5)}。
(2)设会员卡支付金额y(元)关于骑行时间x(时)的函数表达式为y = ax(a ≠ 0)。将(1, 0.75)代入，得a×1 = 0.75，解得a = 0.75。
∴会员卡支付金额y(元)关于骑行时间x(时)的函数表达式为y = 0.75x。根据题意，得0.75x = x - 0.5，解得x = 2。
∴当骑行时间为2小时时，两种支付方式支付的金额相同。
(3)当x = 2.5时，用会员卡支付需0.75×2.5 = 1.875(元)；用手机支付需2.5 - 0.5 = 2(元)。
∵1.875 ＜ 2，
∴选择会员卡支付比较合算。