《2025年通城学典课时作业本八年级数学下册华师大版》

1. 下列函数中，一定是一次函数的为( )
A. y = 5x² + 3
B. y = -$\frac{x}{2}$
C. y = $\frac{5}{x}$
D. y = kx + b

答案： B

2. 若 y = (m - 1)x^|m| + 2 是关于 x 的一次函数，则其图象不经过( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限

答案： C

3. (2024. 海口龙华期中) 把函数 y = -2x - 1 的图象向上平移 3 个单位，则下列各坐标所表示的点中，在平移后的直线上的是( )
A. (2, 2)
B. (2, 3)
C. (2, -2)
D. (2, 5)

答案： C

4. 在一次函数 y = (2m - 1)x + 2 中，y 随 x 的增大而增大，则点 P(-m, m) 在( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限

答案： B

5. (2024. 南阳新野期末) 某生物小组观察一植物的生长情况，得到植物高度 y(厘米)与观察时间 x(天)之间的关系，并画出如图所示的图象(AC 是线段，射线 CD 平行于 x 轴)。下列说法中，错误的是( )

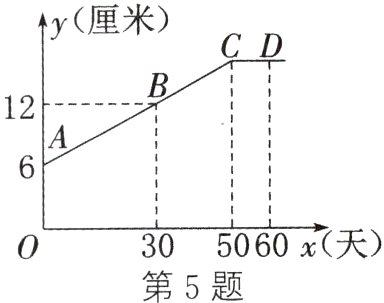
A. AC 所在直线对应的函数表达式为 y = $\frac{1}{5}$x + 6
B. 该植物的高度最高为 16 厘米
C. 从开始观察时算起，60 天后该植物停止长高
D. 第 40 天该植物的高度为 14 厘米

答案： C　解析:由题图，可知AC所在直线经过点(0,6)，故可设其对应的函数表达式为y = kx + 6(k≠0)。将(30,12)代入，得30k + 6 = 12，解得k = $\frac{1}{5}$。
∴AC所在直线对应的函数表达式为y = $\frac{1}{5}$x + 6。故选项A正确，不合题意。由y = $\frac{1}{5}$x + 6，可知当x = 50时，y = $\frac{1}{5}$×50 + 6 = 16。故选项B正确，不合题意。由题图，可知从开始观察时算起，50天后该植物停止长高。故选项C错误，符合题意。由y = $\frac{1}{5}$x + 6，可知当x = 40时，y = $\frac{1}{5}$×40 + 6 = 14，
∴第40天该植物的高度为14厘米。故选项D正确，不合题意。

6. 飞机从 1200 米的高空开始下降，每秒下降 150 米，则飞机离地面的高度 h(米)与时间 t(秒)之间的函数表达式为________________。

答案： h = -150t + 1200(0≤t≤8)

7. (2024. 衡阳期末) 在平面直角坐标系中，若将一次函数 y = -2x + m 的图象向下平移 3 个单位后经过原点，则 m 的值为________。

答案： 3

8. (2024. 长春二道期末) 函数 y = kx + b(k ≠ 0) 的图象上有 A(x₁, y₁)、B(x₂, y₂) 两点，当 x₁ ＞ x₂ 时，y₁ ＜ y₂，写出一个满足条件的函数表达式:____________。

答案： 答案不唯一，如y = -2x + 1

9. (2024. 新乡期末) 已知点 A(m, y₁)、B(m + 1, y₂) 均在一次函数 y = x + b 的图象上，则 y₁ 与 y₂ 的大小关系是________(用“＜”连接)。

答案： y1＜y2

10. 在平面直角坐标系中，点 A(2, m) 在直线 y = -2x + 1 上，点 A 关于 y 轴的对称点 B 恰好落在直线 y = kx + 1 上，则 k 的值为________。

答案： 2

11. 如图，直线 y = $\frac{2}{3}$x + 2 分别与 x 轴、y 轴交于点 A、B，以线段 AB 为边，在第二象限内作等腰直角三角形 ABC，且∠BAC = 90°，则过 B、C 两点的直线对应的函数表达式为____________。

答案：
y = -$\frac{1}{5}$x + 2　解析:在y = $\frac{2}{3}$x + 2中，令x = 0，得y = 2，即B(0,2)；令y = 0，得x = -3，即A(-3,0)。
∴OB = 2，OA = 3。如图，过点C作CM⊥x轴于点M，则∠AMC = ∠BOA = 90°。
∴∠ACM + ∠CAM = 90°。
∵△ABC为等腰直角三角形，且∠BAC = 90°，
∴AC = BA，∠CAM + ∠BAO = 90°。
∴∠ACM = ∠BAO。在△CAM和△ABO中，
$\begin{cases}\angle AMC = \angle BOA \\\angle ACM = \angle BAO \\AC = BA\end{cases}$
∴△CAM≌△ABO。
∴MA = OB = 2，MC = OA = 3。
∴OM = OA + MA = 3 + 2 = 5。
∴C(-5,3)。设过B、C两点的直线对应的函数表达式为y = kx + b(k≠0)。将B(0,2)、C(-5,3)代入，得$\begin{cases}b = 2 \\ -5k + b = 3\end{cases}$，解得$\begin{cases}k = -\frac{1}{5} \\ b = 2\end{cases}$。
∴过B、C两点的直线对应的函数表达式为y = -$\frac{1}{5}$x + 2。

12. 已知一次函数 y = (6 + 3m)x + (n - 4)。
(1) 当 m、n 为何值时，y 随 x 的增大而减小?
(2) 当 m、n 为何值时，该函数的图象与 y 轴的交点在 x 轴的下方?
(3) 当 m、n 为何值时，该函数的图象经过原点？

答案：
(1)由题意，得6 + 3m＜0，解得m＜ -2。
∴当m＜ -2，n为任何实数时，y随x的增大而减小。
(2)由题意，得6 + 3m≠0，n - 4＜0，解得m≠ -2，n＜4。
∴当m≠ -2，n＜4时，该函数的图象与y轴的交点在x轴的下方。
(3)由题意，得6 + 3m≠0，n - 4 = 0，解得m≠ -2，n = 4。
∴当m≠ -2，n = 4时，该函数的图象经过原点。