《2025年通城学典课时作业本八年级数学下册华师大版》

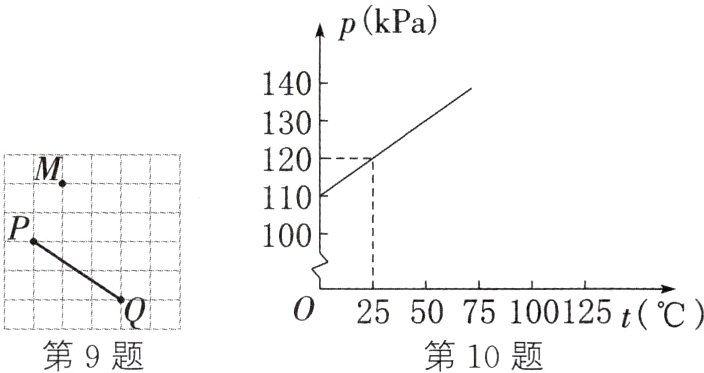
9. 如图，在方格纸中，点P、Q、M的坐标分别记为(0, 2)、(3, 0)、(1, 4)。若MN//PQ，则点N的坐标可能是（ ）

A. (2, 3)
B. (3, 3)
C. (4, 2)
D. (5, 1)

答案： C解析：设直线PQ对应的函数表达式为$y_1 = kx + b(k≠0)$。把(0,2)、(3,0)代入，得$\begin{cases}b = 2 \\ 3k + b = 0 \end{cases}$，解得$k = -\frac{2}{3}$，$b = 2$。
∴直线PQ对应的函数表达式为$y_1 = -\frac{2}{3}x + 2$。
∵MN//PQ，
∴设直线MN对应的函数表达式为$y_2 = -\frac{2}{3}x + t$。
∵M(1,4)，
∴$4 = -\frac{2}{3} + t$，解得$t = \frac{14}{3}$。
∴直线MN对应的函数表达式为$y_2 = -\frac{2}{3}x + \frac{14}{3}$。当x = 2时，$y_2 = \frac{10}{3}$；当x = 3时，$y_2 = \frac{8}{3}$；当x = 4时，$y_2 = 2$；当x = 5时，$y_2 = \frac{4}{3}$。
∴点N的坐标可能是(4,2)。

10. (教材P50例4变式) 研究发现，一定质量的某气体在体积不变的情况下，压强p(kPa)随温度t(℃)变化的函数表达式为p = kt + b (k≠0)，其图象如图所示。当压强为170kPa时，该气体的温度是________°C。

答案： 150 解析：由题图，可知函数p = kt + b的图象经过点(0,110)、(25,120)，
∴$\begin{cases}b = 110 \\ 25k + b = 120 \end{cases}$，解得$k = \frac{2}{5}$，$b = 110$。
∴$p = \frac{2}{5}t + 110(t≥0)$。当p = 170时，$\frac{2}{5}t + 110 = 170$，解得t = 150，即当压强为170kPa时，该气体的温度是150℃。

11. 某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准，该市的用户每月应缴水费y(元)是用水量x(立方米)的函数，其图象如图所示。
(1) 若小明家某月的用水量为18立方米，则应缴水费多少元？
(2) 求当x＞18时，y关于x的函数表达式。若小敏家某月缴水费81元，则她家该月的用水量为多少立方米?

答案：
(1)由题图，可知用水量为18立方米时，应缴水费45元。
(2)设用水量超过18立方米时的函数表达式为y = kx + b(k≠0,x＞18)。由题图，可知函数图象经过点(18,45)、(28,75)，
∴$\begin{cases}18k + b = 45 \\ 28k + b = 75 \end{cases}$，解得$k = 3$，$b = -9$。
∴函数表达式为y = 3x - 9(x＞18)。
∵81＞45，
∴该月用水量超过18立方米。当y = 81时，3x - 9 = 81，解得x = 30。
∴她家该月的用水量为30立方米。

12. 如图，一次函数y = x + 2的图象与x轴、y轴分别交于点A、B，M(1, m)是直线AB上一点，直线MC交x轴于点C($\frac{5}{2}$, 0)。
(1) 求直线MC对应的函数表达式。
(2) P是线段AC上一点(不与点A、C重合)，连结BP、MP。若△ABP的面积是△MPC面积的2倍，求点P的坐标。

答案：
(1)由题意，可知直线AB对应的函数表达式为y = x + 2。
∵M(1,m)是直线AB上一点，
∴将M(1,m)代入y = x + 2，得1 + 2 = m。
∴m = 3。
∴M(1,3)。设直线MC对应的函数表达式为y = kx + b(k≠0)。将M(1,3)、$C(\frac{5}{2},0)$代入y = kx + b，得$\begin{cases}k + b = 3 \\ \frac{5}{2}k + b = 0 \end{cases}$，解得$\begin{cases}k = -2 \\ b = 5 \end{cases}$。
∴直线MC对应的函数表达式为y = -2x + 5。
(2)设点P的坐标为(a,0)。
∵一次函数y = x + 2的图象与x轴、y轴分别交于点A、B，
∴易得A(−2,0)、B(0,2)。
∴AP = a + 2，$PC = \frac{5}{2} - a$。
∴$S_{\triangle ABP} = \frac{1}{2}AP\cdot OB = \frac{1}{2}×(a + 2)×2 = a + 2$，$S_{\triangle MPC} = \frac{1}{2}PC\cdot y_M = \frac{1}{2}×(\frac{5}{2} - a)×3 = \frac{15}{4} - \frac{3}{2}a$。
∵△ABP的面积是△MPC面积的2倍，
∴$a + 2 = 2×(\frac{15}{4} - \frac{3}{2}a)$，解得$a = \frac{11}{8}$。
∴点P的坐标为$(\frac{11}{8},0)$。