《2025年通城学典课时作业本八年级数学下册华师大版》

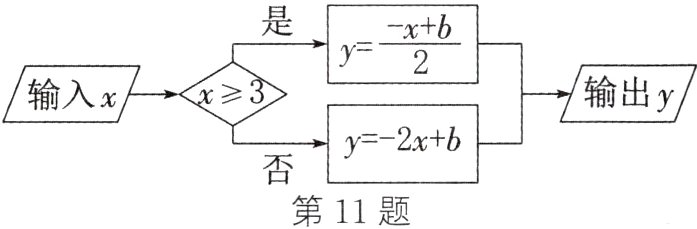
11. 根据如图所示的程序计算函数值，若输入x的值是7，则输出y的值是 -2。若输入x的值是 -8，则输出y的值是(　　　)

A. 5
B. 10
C. 19
D. 21

答案： C

12. 如图，在△ABC中，边BC的长是10，边BC上的高是6，点D在边BC上运动(点D不与点B、C重合)。设BD的长为x，则△ACD的面积y与x之间的函数表达式为__________________，自变量x的取值范围是____________。

答案： y = -3x + 30　0＜x＜10

13. 拖拉机开始工作时，油箱中有40L油，已知拖拉机工作时每小时耗油4L。设油箱中的剩余油量为QL，工作时间为th。
(1) 写出Q与t之间的函数表达式。
(2) 分别计算当t = 5和t = 10时的Q的值，并说明它们表示的意义。
(3) 拖拉机能工作12h吗？为什么？

答案：
(1)Q = 40 - 4t
(2)当t = 5时，Q = 40 - 4×5 = 20，表示工作5h后油箱中的剩余油量为20L；当t = 10时，Q = 40 - 4×10 = 0，表示工作10h后油箱中的剩余油量为0L
(3)不能。
∵拖拉机工作10h后，油箱中的剩余油量为0L，
∴拖拉机最多只能工作10h，不能工作12h

14. (教材P32例2变式)如图，在长方形MNPQ中，MN = 6，PN = 4，动点R从点N出发，沿N→P→Q→M的方向运动至点M处停止。设点R运动的路程为x，△MNR的面积为y。
(1) 分别求当0＜x＜4、4≤x≤10、10＜x＜14时，y与x之间的函数表达式；
(2) 当y = 6时，x = ________。

答案：
(1)当0＜x＜4时，动点R在NP上运动，y = $\frac{1}{2}$MN·RN = $\frac{1}{2}$×6·x = 3x；当4≤x≤10时，动点R在PQ上运动，y = $\frac{1}{2}$MN·PN = $\frac{1}{2}$×6×4 = 12；当10＜x＜14时，动点R在QM上运动，y = $\frac{1}{2}$MN·RM = $\frac{1}{2}$×6×[4 - (x - 4 - 6)] = 42 - 3x
(2)2或12