《2025年通城学典课时作业本八年级数学下册华师大版》

25. 人体血液中，白细胞的直径约为1.0×10⁻⁵cm，红细胞的直径约是白细胞直径的77%，则红细胞的直径用科学记数法表示为________cm。

答案： 7.7×10⁻⁴

26. 已知$\frac{1}{p} - \frac{1}{q} = 2$，则分式$\frac{3p - pq - 3q}{2p + pq - 2q}$的值为________。

答案： $\frac{7}{3}$

27. 若a、b互为倒数，则代数式$\frac{a^2 + 2ab + b^2}{a + b} \div (\frac{1}{a} + \frac{1}{b})$的值为________。

答案： 1

28. 若分式方程$\frac{x}{x - 1} = 3 - \frac{mx}{1 - x}$的解为正整数，则整数m的值为________。

答案： -1解析：方程两边同乘以(x - 1)，得x = 3(x - 1)+mx，
展开得x = 3x - 3+mx，
移项得x - 3x - mx=-3，
合并同类项得(-2 - m)x=-3，解得x = $\frac{3}{2 + m}$。
∵方程的解为正整数且m为整数，
∴2 + m是3的正因数，即2 + m = 1或2 + m = 3，解得m = -1或m = 1。
当m = 1时，x = 1，此时x - 1 = 0，分式方程无意义，
∴m = 1不合题意，应舍去。
∴m的值为-1。

29. 先化简，再求值：$\frac{2}{x^2 + x} \div (1 - \frac{x - 1}{x^2 - 1})$，其中x是不等式组$\begin{cases}2x - 3 \geq 1 \\ x + 1 ＜ 2x \end{cases}$的整数解。

答案： $\frac{2}{x² + x}$+(1 - $\frac{x - 1}{x² - 1}$)=$\frac{2}{x(x + 1)}$+$\frac{x² - 1 - x + 1}{(x + 1)(x - 1)}$=$\frac{2}{x(x + 1)}$+$\frac{x(x - 1)}{(x + 1)(x - 1)}$=$\frac{2}{x(x + 1)}$+$\frac{x}{x + 1}$=$\frac{2 + x²}{x(x + 1)}$
解不等式2(x - 1)＜x + 1，得2x - 2＜x + 1，2x - x＜1 + 2，x＜3；
解不等式5x + 3≥2x，得5x - 2x≥-3，3x≥-3，x≥-1，
∴不等式组的解集为-1≤x＜3。
∵x为整数，
∴x的值为-1或0或1或2。
∵x≠0且(x + 1)(x - 1)≠0，
∴x≠0且x≠±1。
∴x只能取2。
当x = 2时，原式=$\frac{2 + 2²}{2×(2 + 1)}$=$\frac{6}{6}$ = 1

30. 已知$y = \frac{x}{x^2 - x} \div \frac{x^2 - 1}{x^2 - 2x + 1} - \frac{2}{x + 1}$，则当x为何值时，y的值为$\frac{1}{3}$？

答案： y = $\frac{x}{x² - x}$+$\frac{x² - 1}{x² - 2x + 1}$-$\frac{2}{x + 1}$=$\frac{x}{x(x - 1)}$+$\frac{(x + 1)(x - 1)}{(x - 1)²}$-$\frac{2}{x + 1}$=$\frac{1}{x - 1}$+$\frac{x + 1}{x - 1}$-$\frac{2}{x + 1}$=$\frac{x + 2}{x - 1}$-$\frac{2}{x + 1}$=$\frac{(x + 2)(x + 1)-2(x - 1)}{(x - 1)(x + 1)}$=$\frac{x² + 3x + 2 - 2x + 2}{(x - 1)(x + 1)}$=$\frac{x² + x + 4}{(x - 1)(x + 1)}$
由题意，得$\frac{x² + x + 4}{(x - 1)(x + 1)}$=$\frac{1}{3}$，
交叉相乘得3(x² + x + 4)=(x - 1)(x + 1)，
3x² + 3x + 12 = x² - 1，
2x² + 3x + 13 = 0，
判别式$\Delta$ = 3² - 4×2×13 = 9 - 104=-95＜0，此方程无实数解。原题目可能存在错误。

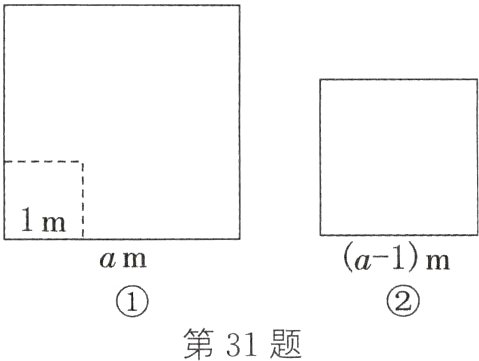
31. 如图①，“优选1号”水稻的试验田是边长为am（a＞1）的正方形去掉一个边长为1m的正方形蓄水池后余下的部分；如图②，“优选2号”水稻的试验田是边长为(a - 1)m的正方形，两块试验田的水稻都收了600kg。
(1) 哪种水稻单位面积的产量更高？
(2) “优选2号”水稻单位面积的产量是“优选1号”水稻单位面积的产量的多少倍？

答案：
(1)由题意，得“优选1号”水稻单位面积的产量为$\frac{600}{a² - 1}$kg/m²，“优选2号”水稻单位面积的产量为$\frac{600}{(a - 1)²}$kg/m²。
∵$\frac{600}{a² - 1}$-$\frac{600}{(a - 1)²}$=600·$\frac{a - 1-(a + 1)}{(a + 1)(a - 1)²}$=600·$\frac{-2}{(a + 1)(a - 1)²}$＜0，
∴$\frac{600}{a² - 1}$＜$\frac{600}{(a - 1)²}$，即“优选2号”水稻单位面积的产量更高
(2)由题意，得$\frac{\frac{600}{(a - 1)²}}{\frac{600}{a² - 1}}$=$\frac{600}{(a - 1)²}$×$\frac{a² - 1}{600}$=$\frac{(a + 1)(a - 1)}{(a - 1)²}$=$\frac{a + 1}{a - 1}$。
∴“优选2号”水稻单位面积的产量是“优选1号”水稻单位面积的产量的$\frac{a + 1}{a - 1}$倍