《2025年1加1轻巧夺冠优化训练七年级数学下册人教版银版》

3 若$a ＜ b$，则$a + 2$______$b + 2$（填“＜”或“＞”）.

答案： ＜

13（2024·长春）不等关系在生活中广泛存在.如图，$a$，$b$分别表示两位同学的身高，$c$表示台阶的高度.图中两人的对话体现的数学原理是（ ）

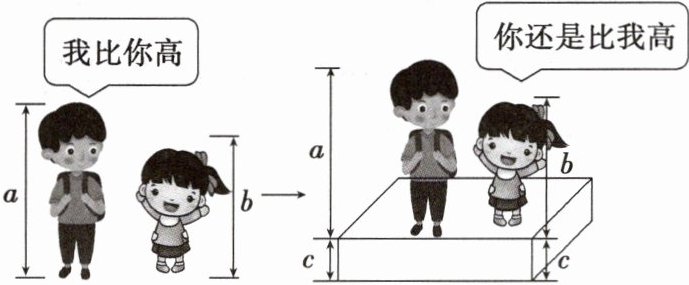
A.若$a ＞ b$，则$a + c ＞ b + c$
B.若$a ＞ b$，$b ＞ c$，则$a ＞ c$
C.若$a ＞ b$，$c ＞ 0$，则$ac ＞ bc$
D.若$a ＞ b$，$c ＞ 0$，则$\frac{a}{c}＞\frac{b}{c}$

答案： A

14 实数$a$，$b$，$c$满足$a ＞ b$，且$ac ＞ bc$，它们在数轴上的对应点的位置可以是（ ）

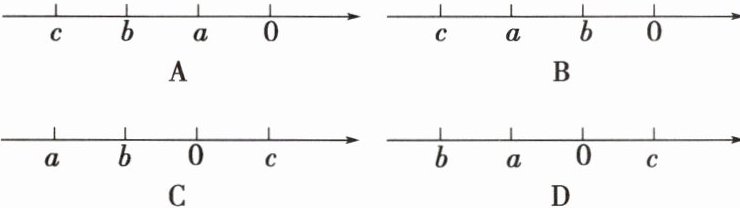
答案： D

15（2024·安庆一模）已知$a$，$b$，$c$为非零实数，且满足$a + b + c = 0$，$4a + 2b + c ＜ 2$，则下列结论一定正确的是（ ）
A.$2a - c ＞ 2$
B.$3a - b - 3c ＜ 4$
C.$3a ＜ 2$
D.$a + 3b + 4c ＞ 0$

答案： B

16（2024·邓州二模）若不等式$(m - 3)x ＜ 3 - m$的两边同除以$(m - 3)$，得$x ＞ - 1$，则$m$的取值范围为______.

答案： $m ＜ 3$

17 已知关于$x$的不等式$(m - 1)x ＞ 6$，两边同除以$m - 1$，得$x ＜\frac{6}{m - 1}$，试化简：$|m - 1| - |2 - m|$.

答案： 解：因为关于 $x$的不等式$(m - 1)x＞6$，两边同除以 $m - 1$，得 $x＜\frac{6}{m - 1}$，
所以 $m - 1 ＜ 0$，所以 $m ＜ 1$，所以 $2 - m＞1$.
所以$\vert m - 1\vert-\vert 2 - m\vert=(1 - m)-(2 - m)=1 - m - 2 + m=-1$.

18 阅读下面的材料：
小明在学习了不等式的知识后，发现如下正确结论：
若$A - B ＞ 0$，则$A ＞ B$；
若$A - B = 0$，则$A = B$；
若$A - B ＜ 0$，则$A ＜ B$.
下面是小明利用这个结论解决问题的过程：
试比较$\sqrt{3}$与$2\sqrt{2}-\sqrt{3}$的大小.
解：$\because\sqrt{3}-(2\sqrt{2}-\sqrt{3})$
$=\sqrt{3}-2\sqrt{2}+\sqrt{3}$
$=2\sqrt{3}-2\sqrt{2}＞0$，
$\therefore\sqrt{3}$______$2\sqrt{2}-\sqrt{3}$.
解答下列问题：
（1）请完成小明的解题过程；
（2）试比较$2(x^{2}-3xy + 4y^{2})-3$与$3x^{2}-6xy + 8y^{2}-2$的大小.（写出相应的解答过程）

答案： 解：
(1)＞
(2)$2(x^{2}-3xy + 4y^{2})-3-(3x^{2}-6xy + 8y^{2}-2)=2x^{2}-6xy + 8y^{2}-3 - 3x^{2}+6xy - 8y^{2}+2=-x^{2}-1$.
$\because x^{2}\geqslant0$，$\therefore -x^{2}\leqslant0$.
$\therefore -x^{2}-1\leqslant -1$.
$\therefore 2(x^{2}-3xy + 4y^{2})-3-(3x^{2}-6xy + 8y^{2}-2)＜0$，
即 $2(x^{2}-3xy + 4y^{2})-3＜3x^{2}-6xy + 8y^{2}-2$.