2025年1加1轻巧夺冠优化训练七年级数学下册人教版银版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠优化训练七年级数学下册人教版银版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1 下列方程中,属于三元一次方程的是( )
A. $\pi +x + y = 6$
B. $xy + y + z = 7$
C. $x + 2y - 3z = 9$
D. $3x + 2y - 4z = 4x + 2y - 2z$
A. $\pi +x + y = 6$
B. $xy + y + z = 7$
C. $x + 2y - 3z = 9$
D. $3x + 2y - 4z = 4x + 2y - 2z$
答案:
C
2 下列是三元一次方程组的是( )
A. $\begin{cases}2x = 5, \\x^{2}+y = 7, \\x + y + z = 6\end{cases}$
B. $\begin{cases}\frac{3}{x}-y + z = -2, \\x - 2y + z = 9, \\y = -3\end{cases}$
C. $\begin{cases}x + y - z = 7, \\xyz = 1, \\x - 3y = 4\end{cases}$
D. $\begin{cases}x + y = 2, \\y + z = 1, \\x + z = 9\end{cases}$
A. $\begin{cases}2x = 5, \\x^{2}+y = 7, \\x + y + z = 6\end{cases}$
B. $\begin{cases}\frac{3}{x}-y + z = -2, \\x - 2y + z = 9, \\y = -3\end{cases}$
C. $\begin{cases}x + y - z = 7, \\xyz = 1, \\x - 3y = 4\end{cases}$
D. $\begin{cases}x + y = 2, \\y + z = 1, \\x + z = 9\end{cases}$
答案:
D
3 (2024·拱墅区一模)已知方程组$\begin{cases}x + y = 4, \\y + z = 6, \\z + x = 8,\end{cases}$则$x + y + z$的值是( )
A. 9
B. 8
C. 7
D. 6
A. 9
B. 8
C. 7
D. 6
答案:
A
4 (2024·惠安期中)三元一次方程组$\begin{cases}x + y + z = 13, \\y + z = 10, \\x + y - 2z = -5\end{cases}$的解是________.
答案:
$\begin{cases}x = 3,\\y = 4,\\z = 6\end{cases}$
5 若$(a + 1)x + 5y^{b + 1}+2z^{2 - |a|}=10$是一个三元一次方程,则( )
A. $a = 1,b = 0$
B. $a = -1,b = 0$
C. $a = 0,b = 0$
D. $a = \pm1,b = 0$
A. $a = 1,b = 0$
B. $a = -1,b = 0$
C. $a = 0,b = 0$
D. $a = \pm1,b = 0$
答案:
A
6 (2024·唐山二模)如图,两个天平都平衡,则与1个“ ”质量相等的“
”质量相等的“ ”的个数为( )
”的个数为( )
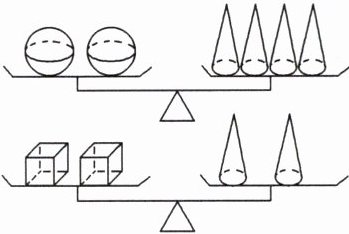
A. 4
B. 3
C. 2
D. 1
 ”质量相等的“
”质量相等的“ ”的个数为( )
”的个数为( )
A. 4
B. 3
C. 2
D. 1
答案:
C
7 【数学问题】解方程组$\begin{cases}x + y = 2,①\\5x - 2(x + y)=6.②\end{cases}$
【思路分析】小明观察后发现方程①的左边是$x + y$,而方程②的括号里也是$x + y$,他想到可以把$x + y$视为一个整体,把方程①直接代入到方程②中,这样,就可以将方程②直接转化为一元一次方程,从而达到“消元”的目的.
(1)【完成解答】请你按照小明的思路,完成解方程组的过程.
(2)你还能用其他的方法来求得方程组的解吗?
(3)【迁移运用】请你按照小明的方法,解方程组$\begin{cases}a + b = 3,①\\5a + 3c = 1,②\\a + b + c = 0.③\end{cases}$
【思路分析】小明观察后发现方程①的左边是$x + y$,而方程②的括号里也是$x + y$,他想到可以把$x + y$视为一个整体,把方程①直接代入到方程②中,这样,就可以将方程②直接转化为一元一次方程,从而达到“消元”的目的.
(1)【完成解答】请你按照小明的思路,完成解方程组的过程.
(2)你还能用其他的方法来求得方程组的解吗?
(3)【迁移运用】请你按照小明的方法,解方程组$\begin{cases}a + b = 3,①\\5a + 3c = 1,②\\a + b + c = 0.③\end{cases}$
答案:
解:
(1)把①代入②,得$5x - 2×2 = 6$,
解得$x = 2$.
把$x = 2$代入①得$2 + y = 2$,
解得$y = 0$.
∴原方程组的解为$\begin{cases}x = 2,\\y = 0\end{cases}$.
(2)由①得$x = 2 - y$,③
把③代入②,得$5(2 - y)-2(2 - y + y)=6$,
解得$y = 0$,
把$y = 0$代入①,得$x = 2$.
∴原方程组的解为$\begin{cases}x = 2,\\y = 0\end{cases}$.
(3)把①代入③,得$3 + c = 0$,
解得$c = - 3$.
把$c = - 3$代入②,得$5a - 9 = 1$,解得$a = 2$.
把$a = 2$代入①,得$2 + b = 3$,解得$b = 1$.
∴原方程组的解为$\begin{cases}a = 2,\\b = 1,\\c = - 3\end{cases}$.
(1)把①代入②,得$5x - 2×2 = 6$,
解得$x = 2$.
把$x = 2$代入①得$2 + y = 2$,
解得$y = 0$.
∴原方程组的解为$\begin{cases}x = 2,\\y = 0\end{cases}$.
(2)由①得$x = 2 - y$,③
把③代入②,得$5(2 - y)-2(2 - y + y)=6$,
解得$y = 0$,
把$y = 0$代入①,得$x = 2$.
∴原方程组的解为$\begin{cases}x = 2,\\y = 0\end{cases}$.
(3)把①代入③,得$3 + c = 0$,
解得$c = - 3$.
把$c = - 3$代入②,得$5a - 9 = 1$,解得$a = 2$.
把$a = 2$代入①,得$2 + b = 3$,解得$b = 1$.
∴原方程组的解为$\begin{cases}a = 2,\\b = 1,\\c = - 3\end{cases}$.
查看更多完整答案,请扫码查看


