《2025年1加1轻巧夺冠优化训练七年级数学下册人教版银版》

18 点P坐标是（5，2），则点P到直线x = -1的距离是_______.

答案： 6

19（2024·营口期末）在如图所示的方格纸上建立适当的平面直角坐标系，若点A的坐标为（0，1），点B的坐标为（1，3），则点C的坐标为_______.

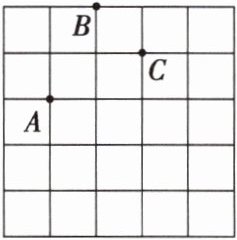
答案： (2, 2)

20 如果点P（x，y）的坐标满足x + y = xy，那么称点P为“和谐点”. 若某个“和谐点”到x轴的距离为3，则该点的坐标为_______.

答案： ($\frac{3}{2}$, 3)或($\frac{3}{4}$, -3)

21（2024·吴江区二模）已知点P（2a - 2，a + 5），回答下列问题：
（1）若点P在y轴上，求出点P的坐标；
（2）若点P在第二象限，且它到x轴、y轴的距离相等，求a²⁰²⁴ + 2024的值.

答案： 解:
(1)
∵点P在y轴上,
∴2a - 2 = 0, 解得a = 1.
∴a + 5 = 6,
∴P(0, 6).
(2)
∵点P到x轴和y轴距离相等,
∴|2a - 2| = |a + 5|.
∵点P在第二象限,
∴2a - 2 ＜ 0, a + 5 ＞ 0.
∴|2a - 2| = 2 - 2a, |a + 5| = a + 5.
∴2 - 2a = a + 5, 解得a = -1.
∴$a^{2024}+2024=(-1)^{2024}+2024 = 2025$.

22（2024·长汀期中）在平面直角坐标系中，给出如下定义：点P到x轴、y轴的距离的较大值称为点P的“长距”，点Q到x轴、y轴的距离相等时，称点Q为“完美点”.
（1）点A（-1，2）的“长距”为_______；
（2）若点B（2a - 1，-1）是“完美点”，求a的值；
（3）若点C（3b - 2，-2）的长距为4，且点C在第四象限内，点D的坐标为（-5，9 - 2b），试说明点D是“完美点”.

答案： 解:
(1) 根据题意, 得点A(-1, 2)到x轴的距离为2, 到y轴的距离为1,
∴点A的“长距”为2. 故答案为2.
(2)
∵点B(2a - 1, -1)是“完美点”,
∴|2a - 1| = | -1|,
∴2a - 1 = 1或2a - 1 = -1,
解得a = 1或a = 0.
(3)
∵点C(3b - 2, -2)的长距为4, 且点C在第四象限内,
∴3b - 2 = 4, 解得b = 2.
∴9 - 2b = 5.
∴点D的坐标为(-5, 5).
∴点D到x轴、y轴的距离都是5.
∴点D是“完美点”.

23（2024·凉州区月考）如图，在平面直角坐标系中，已知A（a，0），B（b，0），其中a，b满足$\sqrt{a + 1}+(b - 3)^2 = 0$.
　
　　
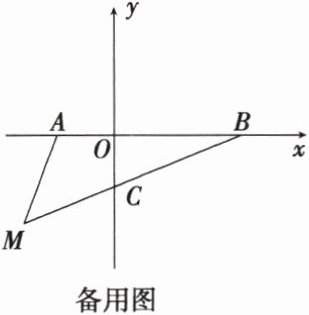
（1）填空：a = _______，b = _______.
（2）若在第三象限内有一点M（-2，m），用含m的式子表示三角形ABM的面积.
（3）在（2）的条件下，线段BM与y轴相交于C（0，-$\frac{9}{10}$），当m = -$\frac{3}{2}$时，点P是y轴上的动点，当满足三角形PBM的面积是三角形ABM的面积的2倍时，求点P的坐标.

答案： 解:
(1)
∵a, b满足$\sqrt{a + 1}+(b - 3)^2 = 0$,
∴a + 1 = 0, 且b - 3 = 0.
∴a = -1, b = 3.
故答案为-1, 3.
(2)
∵a = -1, b = 3,
∴A(-1, 0), B(3, 0),
∴AB = 4.
∵M(-2, m), 且M在第三象限,
∴m ＜ 0.
∴三角形ABM的面积=$\frac{1}{2}×4×(-m)= -2m$.
(3) 当m = -$\frac{3}{2}$时, M(-2, -$\frac{3}{2}$),
$S_{三角形ABM}=-2m=-2×(-\frac{3}{2}) = 3$.
∵三角形PBM的面积 = 三角形ABM的面积的2倍 = 6,
∴三角形PBM的面积 = 三角形MPC的面积 + 三角形BPC的面积=$\frac{1}{2}PC×2+\frac{1}{2}PC×3 = 6$,
解得PC = $\frac{12}{5}$,
∵C(0, -$\frac{9}{10}$),
∴OC = $\frac{9}{10}$.
当点P在点C的下方时, P(0, -$\frac{12}{5}-\frac{9}{10}$),
即P(0, -$\frac{33}{10}$);
当点P在点C的上方时, P(0, $\frac{12}{5}-\frac{9}{10}$),
即P(0, $\frac{3}{2}$).
综上所述, 点P的坐标为(0, -$\frac{33}{10}$)或(0, $\frac{3}{2}$).