《2025年1加1轻巧夺冠优化训练七年级数学下册人教版银版》

12. 判断下列说法是否正确.
（1）$\sqrt{64}$的立方根是-2.
（2）$\pm3$是27的立方根.
李蕾认为（1）错误，（2）正确. 李蕾的观点正确吗？如果不正确，请说明理由.

答案： 解：李蕾的观点错误. 理由如下：
$\sqrt{64}$ 的立方根即 8 的立方根为 2，故
(1)错误；
27 的立方根是 3，故
(2)错误.

13. （2024·汉川期末）要生产一种容积为$36\pi$的球形容器，则球形容器的半径$R$的值是（球的体积公式是$V = \frac{4}{3}\pi R^{3}$）（ ）
A. 9
B. 6
C. $\sqrt[3]{36}$
D. 3

答案： D

14. 给出下列各式：$\sqrt[3]{2\frac{10}{27}}=\frac{4}{3}$，$\sqrt[3]{0.001}=0.1$，$-\sqrt[3]{0.001}=0.1$，$\sqrt[3]{(-27)^{3}}=-27$. 其中正确的个数是（ ）
A. 1
B. 2
C. 3
D. 4

答案： C

15. （2024·楚雄州期末）一个数的算术平方根和它的立方根相等，则这个数是（ ）
A. 1
B. 0
C. 1或0
D. 1或0或-1

答案： C

16. （2024·右玉期末）一个数值转换器的原理如图所示，当输入$x$的值是64时，输出$y$的值是（ ）

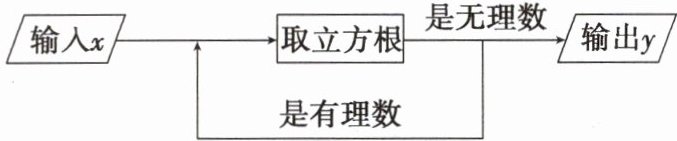
A. 4
B. $\sqrt[3]{4}$
C. 2
D. $\sqrt[3]{2}$

答案： B

17. 已知$a$，$b$都是实数，若$|a - 4|+\sqrt{b + 2}=0$，则$\sqrt[3]{ab}=$______.

答案： -2

18. 比较大小：2______$\sqrt[3]{7}$.

答案： ＞

19. 已知$m$是$\sqrt[3]{13}$的整数部分，$n$是$\sqrt{13}$的小数部分，则$m - n=$______.

答案： $5-\sqrt{13}$

20. 已知$x - 2$的算术平方根是2，$2x + y - 1$的立方根是3，求$y - 2x$的立方根.

答案： 解：$\because x - 2$ 的算术平方根是 2，
$\therefore x - 2 = 4$，解得 $x = 6$.
$\because 2x + y - 1$ 的立方根是 3，
$\therefore 2x + y - 1 = 27$.
又 $\because x = 6$，$\therefore y = 16$，
$\therefore y - 2x = 16 - 2\times6 = 4$，
$\therefore y - 2x$ 的立方根为 $\sqrt[3]{4}$.

21. 化简：
（1）$\sqrt{2^{2}}=$______，$\sqrt{(-2)^{2}}=$______，$\sqrt{0}=$______，$\sqrt{a^{2}}=$______；
（2）$\sqrt[3]{3^{3}}=$______，$\sqrt[3]{(-3)^{3}}=$______，$\sqrt[3]{0}=$______，$\sqrt[3]{a^{3}}=$______；
（3）根据以上信息，观察图中$a$，$b$对应的点在数轴上的位置，试化简：$\sqrt{b^{2}}+\sqrt{(b - a)^{2}}-\sqrt[3]{(a - b)^{3}}$.

答案： 解：
(1) 2 2 0 $|a|$
(2) 3 -3 0 $a$
(3) 由题图可得，$a＜0＜b$，
$\sqrt{b^2}+\sqrt{(b - a)^2}-\sqrt[3]{(a - b)^3}=|b|+|b - a|-(a - b)=b + b - a-(a - b)=b + b - a - a + b = 3b - 2a$.

22. 如果$[x]$表示不大于$x$的最大整数，例如：$[3.15]=3$，$[3.7]=3$，$[3]=3$，则$[\sqrt[3]{1\times2\times3}]+[\sqrt[3]{2\times3\times4}]+[\sqrt[3]{3\times4\times5}]+\cdots+[\sqrt[3]{2021\times2022\times2023}]=$（ ）
A. 2040000
B. 2043000
C. 2043231
D. 2044001

答案： C