《2025年1加1轻巧夺冠优化训练七年级数学下册人教版银版》

13 化简：$\sqrt{(-2)^{2}}=$（ ）
A.$\pm2$
B.$-2$
C.4
D.2

答案： D

14 （2024·建邺区一模）若$\sqrt{a}=4$，则$a$的值为（ ）
A.$-16$
B.16
C.$-2$
D.2

答案： B

15 （2024·陕西）计算：$\sqrt{16}=$_______.

答案： 4

16 当$x=$_______时，$\sqrt{x - 1}$的值最小.

答案： 1

17 如图，若用两个边长为1的小正方形，剪拼成一个大正方形，则该大正方形的边长为_______.

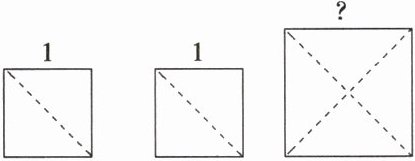
答案： $\sqrt{2}$

18 求下列各式的值：
（1）$\sqrt{1\frac{9}{16}}+\sqrt{36}$；（2）$\sqrt{41^{2}-40^{2}}$；
（3）$\sqrt{0.81}-\sqrt{0.01}$；（4）$\sqrt{1-\frac{9}{25}}$.

答案： 解:
(1)　$\sqrt{1\frac{9}{16}}+\sqrt{36}=\sqrt{\frac{25}{16}}+\sqrt{36}=\frac{5}{4}+6 = 7\frac{1}{4}$.
(2)　$\sqrt{41^{2}-40^{2}}=\sqrt{81}=9$.
(3)　$\sqrt{0.81}-\sqrt{0.01}=0.9 - 0.1 = 0.8$.
(4)$\sqrt{1-\frac{9}{25}}=\sqrt{\frac{16}{25}}=\frac{4}{5}$.

19 已知$2a + 1$的算术平方根是0，$b - a$的算术平方根是$\frac{1}{2}$，求$\frac{1}{2}ab$的算术平方根.

答案： 解:
∵$2a + 1$的算术平方根是0，
∴$2a + 1 = 0$，解得$a = -\frac{1}{2}$.
∵$b - a$的算术平方根是$\frac{1}{2}$，
∴$b - a=\frac{1}{4}$，
∴$b = -\frac{1}{4}$.
∴$\frac{1}{2}ab=\frac{1}{2}×(-\frac{1}{2})×(-\frac{1}{4})=\frac{1}{16}$.
∵$\frac{1}{16}$的算术平方根是$\frac{1}{4}$，
∴$\frac{1}{2}ab$的算术平方根是$\frac{1}{4}$.

20 观察表格回答下列问题.

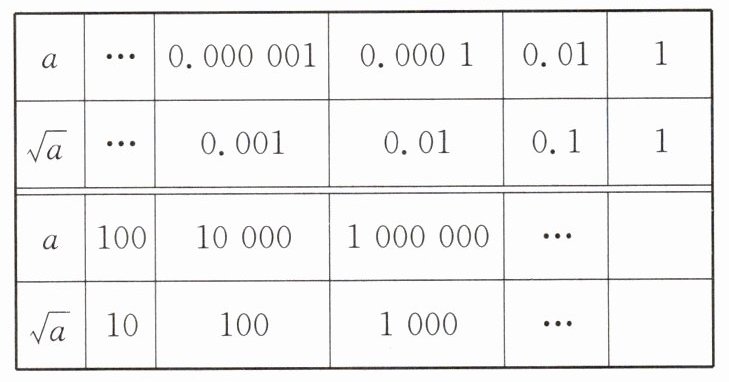
（1）被开方数$a$的小数点位置移动和它的算术平方根$\sqrt{a}$的小数点位置移动有无规律？若有规律，请写出这个移动规律.
（2）已知$\sqrt{3}\approx1.732$，利用（1）中你发现的规律，求出$\sqrt{0.03}$的值.
（3）已知$\sqrt{a}=1800$，$-\sqrt{3.24}=-1.8$，求出$a$的值.
（4）试比较$\sqrt{a}$与$a$的大小（$a\geq0$）.

答案： 解:
(1)有规律.被开方数$a$的小数点位置向左(或向右)移动$2n$（$n$为正整数）位，它的算术平方根$\sqrt{a}$的小数点位置就相应向左(或向右)移动$n$位.
(2)
∵$\sqrt{3}\approx1.732$，
∴　$\sqrt{0.03}\approx0.1732$.
(3)
∵$\sqrt{a}=1800$，$-\sqrt{3.24}=-1.8$.
∴$a = 3240000$.
(4)当$a = 0$或1时，$a=\sqrt{a}$；当$a＞1$时，$a＞\sqrt{a}$；当$0 ＜ a ＜ 1$时，$a＜\sqrt{a}$.