2025年1加1轻巧夺冠优化训练七年级数学下册人教版银版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠优化训练七年级数学下册人教版银版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
8 如图,点O是直线AB上的任意一点,OC,OD,OE是过点O的三条射线,若∠AOD = ∠COE = 90°,有下列说法:
①与∠AOC互为邻补角的角只有一个;
②与∠AOC互为补角的角只有一个;
③与∠AOC互为邻补角的角有两个;
④与∠AOC互为补角的角有两个.
其中正确的是( )

A. ②③
B. ①②
C. ③④
D. ①④
①与∠AOC互为邻补角的角只有一个;
②与∠AOC互为补角的角只有一个;
③与∠AOC互为邻补角的角有两个;
④与∠AOC互为补角的角有两个.
其中正确的是( )

A. ②③
B. ①②
C. ③④
D. ①④
答案:
D
9 如图,直线a,b相交,∠1:∠2 = 2:7,则∠3的度数是( )
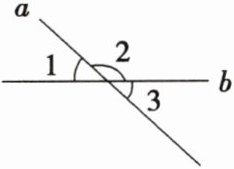
A. 20°
B. 60°
C. 45°
D. 40°

A. 20°
B. 60°
C. 45°
D. 40°
答案:
D
10 平面内两两相交的3条直线,其交点最少为m个,最多为n个,则m + n等于( )
A. 4
B. 5
C. 6
D. 以上都不对
A. 4
B. 5
C. 6
D. 以上都不对
答案:
A
11(2024·唐山三模)如图,直线a与直线b交于点A,此时图中有两对对顶角,若过点A再画一条不与直线a,b重合的直线c,则新增加的对顶角有( )
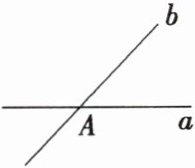
A. 2对
B. 3对
C. 4对
D. 5对

A. 2对
B. 3对
C. 4对
D. 5对
答案:
C
12 如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE. 若∠AOC的度数为2α,则∠EOF = ________.(用含α的代数式表示)
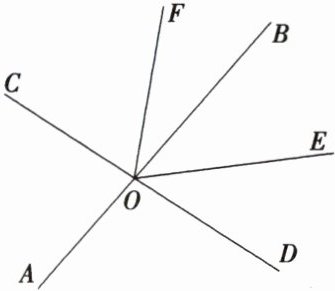

答案:
$90^{\circ}-\frac{\alpha}{2}$
13 如图,直线AB,CD相交于点O,OE平分∠BOC,∠COF = 90°.
(1)若∠BOE = 70°,求∠AOF的度数;
(2)若∠BOD:∠BOE = 1:2,求∠AOF的度数.
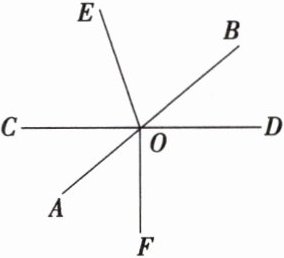
(1)若∠BOE = 70°,求∠AOF的度数;
(2)若∠BOD:∠BOE = 1:2,求∠AOF的度数.

答案:
解:
(1)
∵OE 平分∠BOC,∠BOE = 70°,
∴∠BOC = 2∠BOE = 140°.
∴∠AOC = 180° - 140° = 40°.
∵∠COF = 90°,
∴∠AOF = 90° - 40° = 50°.
(2)
∵OE 平分∠BOC,
∴∠COE = ∠BOE.
∵∠BOD : ∠BOE = 1 : 2,
∴∠BOD : ∠BOC = 1 : 4.
∴∠BOD = $\frac{1}{5}\times180^{\circ}=36^{\circ}$.
∴∠AOC = 36°.
∵∠COF = 90°,
∴∠AOF = 90° - 36° = 54°.
(1)
∵OE 平分∠BOC,∠BOE = 70°,
∴∠BOC = 2∠BOE = 140°.
∴∠AOC = 180° - 140° = 40°.
∵∠COF = 90°,
∴∠AOF = 90° - 40° = 50°.
(2)
∵OE 平分∠BOC,
∴∠COE = ∠BOE.
∵∠BOD : ∠BOE = 1 : 2,
∴∠BOD : ∠BOC = 1 : 4.
∴∠BOD = $\frac{1}{5}\times180^{\circ}=36^{\circ}$.
∴∠AOC = 36°.
∵∠COF = 90°,
∴∠AOF = 90° - 36° = 54°.
14 如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COE.
(1)若∠AOC = 76°,求∠BOF的度数;
(2)若∠BOF = 36°,求∠AOC的度数;
(3)若|∠AOC - ∠BOF| = α,求∠AOC和∠BOF的度数.(用含α的代数式表示)
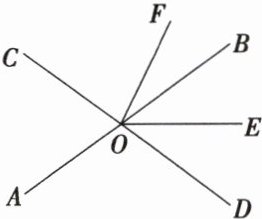
(1)若∠AOC = 76°,求∠BOF的度数;
(2)若∠BOF = 36°,求∠AOC的度数;
(3)若|∠AOC - ∠BOF| = α,求∠AOC和∠BOF的度数.(用含α的代数式表示)

答案:
解:
(1)
∵∠BOD = ∠AOC = 76°,OE 平分∠BOD,
∴∠BOE = ∠DOE = $\frac{1}{2}$∠BOD = $\frac{1}{2}\times76^{\circ}=38^{\circ}$.
∴∠COE = 180° - ∠DOE = 180° - 38° = 142°.
∵OF 平分∠COE,
∴∠EOF = $\frac{1}{2}$∠COE = $\frac{1}{2}\times142^{\circ}=71^{\circ}$.
∴∠BOF = ∠EOF - ∠BOE = 71° - 38° = 33°.
(2)
∵OE 平分∠BOD,OF 平分∠COE,
∴∠BOE = ∠DOE,∠COF = ∠EOF.
设∠BOE = β,则∠DOE = β,
∴∠COA = ∠BOD = 2β,∠EOF = ∠COF = β + 36°.
∴∠AOC + ∠COF + ∠BOF = 2β + β + 36° + 36° = 180°. 解得β = 36°.
∴∠AOC = 72°.
(3)设∠BOE = $x^{\circ}$,则∠DOE = $x^{\circ}$,∠COA = ∠BOD = 2$x^{\circ}$,∠BOC = 180° - 2$x^{\circ}$,∠COF = ∠EOF = $x^{\circ}$ + ∠BOF.
∴∠BOF = ∠BOC - ∠COF = (180° - 2$x^{\circ}$) - ($x^{\circ}$ + ∠BOF),化简得∠BOF = 90° - $\frac{3}{2}x^{\circ}$.
∵|∠AOC - ∠BOF| = α,
∴$\left|2x^{\circ}-\left(90^{\circ}-\frac{3}{2}x^{\circ}\right)\right|=\alpha$,
解得$x^{\circ}=\left(\frac{180}{7}\right)^{\circ}+\frac{2}{7}\alpha$或$x^{\circ}=\left(\frac{180}{7}\right)^{\circ}-\frac{2}{7}\alpha$.
当$x^{\circ}=\left(\frac{180}{7}\right)^{\circ}+\frac{2}{7}\alpha$时,∠AOC = 2$x^{\circ}=\left(\frac{360}{7}\right)^{\circ}+\frac{4}{7}\alpha$,
∠BOF = 90° - $\frac{3}{2}x^{\circ}=\left(\frac{360}{7}\right)^{\circ}-\frac{3}{7}\alpha$.
当$x^{\circ}=\left(\frac{180}{7}\right)^{\circ}-\frac{2}{7}\alpha$时,∠AOC = 2$x^{\circ}=\left(\frac{360}{7}\right)^{\circ}-\frac{4}{7}\alpha$,
∠BOF = 90° - $\frac{3}{2}x^{\circ}=\left(\frac{360}{7}\right)^{\circ}+\frac{3}{7}\alpha$.
综上所述,∠AOC = $\left(\frac{360}{7}\right)^{\circ}+\frac{4}{7}\alpha$,∠BOF = $\left(\frac{360}{7}\right)^{\circ}-\frac{3}{7}\alpha$或∠AOC = $\left(\frac{360}{7}\right)^{\circ}-\frac{4}{7}\alpha$,∠BOF = $\left(\frac{360}{7}\right)^{\circ}+\frac{3}{7}\alpha$.
(1)
∵∠BOD = ∠AOC = 76°,OE 平分∠BOD,
∴∠BOE = ∠DOE = $\frac{1}{2}$∠BOD = $\frac{1}{2}\times76^{\circ}=38^{\circ}$.
∴∠COE = 180° - ∠DOE = 180° - 38° = 142°.
∵OF 平分∠COE,
∴∠EOF = $\frac{1}{2}$∠COE = $\frac{1}{2}\times142^{\circ}=71^{\circ}$.
∴∠BOF = ∠EOF - ∠BOE = 71° - 38° = 33°.
(2)
∵OE 平分∠BOD,OF 平分∠COE,
∴∠BOE = ∠DOE,∠COF = ∠EOF.
设∠BOE = β,则∠DOE = β,
∴∠COA = ∠BOD = 2β,∠EOF = ∠COF = β + 36°.
∴∠AOC + ∠COF + ∠BOF = 2β + β + 36° + 36° = 180°. 解得β = 36°.
∴∠AOC = 72°.
(3)设∠BOE = $x^{\circ}$,则∠DOE = $x^{\circ}$,∠COA = ∠BOD = 2$x^{\circ}$,∠BOC = 180° - 2$x^{\circ}$,∠COF = ∠EOF = $x^{\circ}$ + ∠BOF.
∴∠BOF = ∠BOC - ∠COF = (180° - 2$x^{\circ}$) - ($x^{\circ}$ + ∠BOF),化简得∠BOF = 90° - $\frac{3}{2}x^{\circ}$.
∵|∠AOC - ∠BOF| = α,
∴$\left|2x^{\circ}-\left(90^{\circ}-\frac{3}{2}x^{\circ}\right)\right|=\alpha$,
解得$x^{\circ}=\left(\frac{180}{7}\right)^{\circ}+\frac{2}{7}\alpha$或$x^{\circ}=\left(\frac{180}{7}\right)^{\circ}-\frac{2}{7}\alpha$.
当$x^{\circ}=\left(\frac{180}{7}\right)^{\circ}+\frac{2}{7}\alpha$时,∠AOC = 2$x^{\circ}=\left(\frac{360}{7}\right)^{\circ}+\frac{4}{7}\alpha$,
∠BOF = 90° - $\frac{3}{2}x^{\circ}=\left(\frac{360}{7}\right)^{\circ}-\frac{3}{7}\alpha$.
当$x^{\circ}=\left(\frac{180}{7}\right)^{\circ}-\frac{2}{7}\alpha$时,∠AOC = 2$x^{\circ}=\left(\frac{360}{7}\right)^{\circ}-\frac{4}{7}\alpha$,
∠BOF = 90° - $\frac{3}{2}x^{\circ}=\left(\frac{360}{7}\right)^{\circ}+\frac{3}{7}\alpha$.
综上所述,∠AOC = $\left(\frac{360}{7}\right)^{\circ}+\frac{4}{7}\alpha$,∠BOF = $\left(\frac{360}{7}\right)^{\circ}-\frac{3}{7}\alpha$或∠AOC = $\left(\frac{360}{7}\right)^{\circ}-\frac{4}{7}\alpha$,∠BOF = $\left(\frac{360}{7}\right)^{\circ}+\frac{3}{7}\alpha$.
查看更多完整答案,请扫码查看


