《2025年1加1轻巧夺冠优化训练七年级数学下册人教版银版》

1 (2024·鄂州模拟)如图，直线AB//CD，GE⊥EF于点E.若∠BGE = 60°，则∠EFD的度数是（ ）

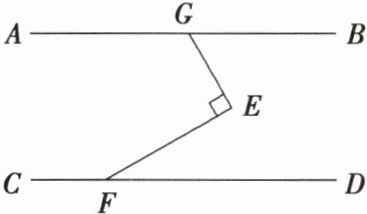
A. 60°
B. 30°
C. 40°
D. 70°

答案： B

2 如图，将一副直角三角板和一张对边平行的纸条按图的方式摆放，两块三角板的一直角边重合，含30°角的直角三角板的斜边与纸条的一边重合，含45°角的直角三角板的一个顶点在纸条的另一边上，则∠1的度数是（ ）

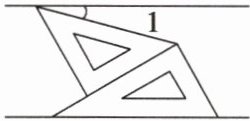
A. 15°
B. 22.5°
C. 30°
D. 45°

答案： A

3 如图，AB//CD，∠A = 120°，∠1 = 70°，则∠D的度数为_______.

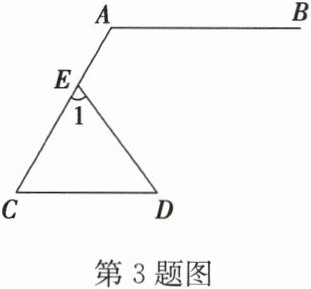
答案： 50°

4 如图，已知AB//DE，∠ABC = 70°，∠CDE = 140°，则∠BCD的度数为_______.

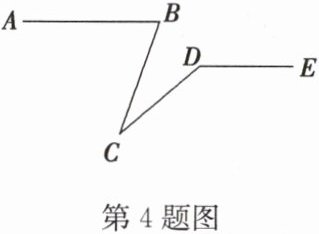
答案： 30°

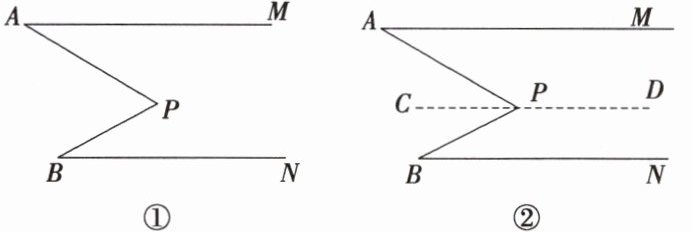
5 已知：如图①，AM//BN，点P是两平行线间的任意一点，连接AP，BP. 小雅猜想∠APB = ∠A + ∠B，并写出了如下的证明过程，请你补充完整.
证明：如图②，过点P作直线CD使得CD//AM，
∴∠A = ∠APC(两直线平行，内错角相等).
∵AM//BN(_______)，
∴CD//_______(平行于同一条直线的两条直线平行).
∴∠B = ∠BPC(______________).
∴∠APB = ∠APC + ∠BPC = ∠A + ∠B(等量代换).

答案： 已知 BN 两直线平行，内错角相等

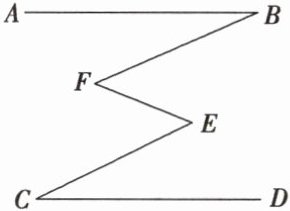
6 如图，AB//CD，∠ABF = ∠DCE. 求证：∠BFE = ∠FEC.

答案：
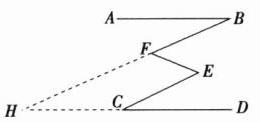
证明:如图，延长 BF 交 DC 的延长线于点 H.
∵AB//CD，
∴∠ABF = ∠H.
∵∠ABF = ∠DCE;
∴∠H = ∠DCE;
∴BH//CE,
∴∠BFE = ∠FEC;

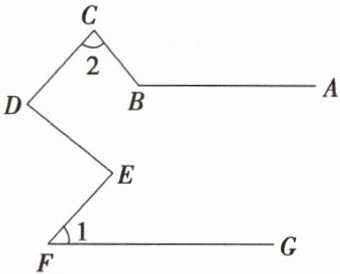
7 如图，已知CD//EF，∠1 + ∠2 = ∠ABC，试判断AB与GF的位置关系，并说明理由.

答案：
解:AB//GF.理由如下:
如图，过点 C 作 CK//GF，延长 GF，CD 交于点 H.
∵CK//FG，
∴∠H + ∠2 + ∠BCK = 180°.
∵CD//EF，
∴∠H = ∠1.
又
∵∠1 + ∠2 = ∠ABC，
∴∠ABC + ∠BCK = 180°.
∴AB//CK.
∵CK//GF，
∴AB//GF.