《2025年1加1轻巧夺冠优化训练七年级数学下册人教版银版》

9. 给出下列关于平行线的四个命题：
①同一平面内不相交的两条直线平行；
②过一点有且仅有一条直线与已知直线平行；
③平行于同一条直线的两条直线平行；
④同一平面内，垂直于同一条直线的两直线互相平行.
其中，真命题的个数是（ ）
A. 1
B. 2
C. 3
D. 4

答案： C

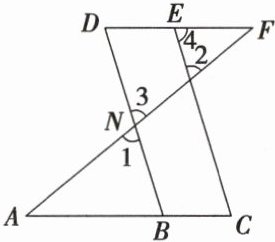
10. 如图，有下列命题：①若$\angle1=\angle2$，则$\angle D=\angle4$；②若$\angle C=\angle D$，则$\angle4=\angle C$；③若$\angle4=\angle F$，则$\angle1=\angle2$；④若$\angle1=\angle2$，$\angle C=\angle D$，则$\angle A=\angle F$；⑤若$\angle C=\angle D$，$\angle A=\angle F$，则$\angle1=\angle2$. 其中，是真命题的有（ ）

A. 1个
B. 2个
C. 3个
D. 4个

答案： C

11. （2024·良庆区校级模拟）命题“等角的余角相等”是________命题.（填“真”或“假”）

答案： 真

12. （2024·新蔡二模）能说明“若$a^{2}＞4$，则$a＞2$”是假命题的一个反例可以是________.

答案： a = -3(答案不唯一)

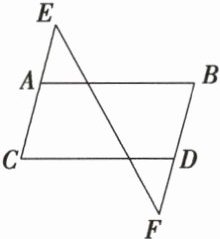
13. 如图，现有以下三个条件：①$AB// CD$；②$\angle B=\angle C$；③$\angle E=\angle F$. 请你以其中两个作为题设，另一个作为结论构造命题.
（1）你构造的是哪几个命题？
（2）你构造的命题是真命题还是假命题？若是真命题，请给予证明；若是假命题，请举出反例.

答案： 解：
(1)如果①②，那么③；如果①③，那么②；如果②③，那么①.
(2)“如果①②，那么③”是真命题. 证明如下：
∵AB//CD，
∴∠B = ∠CDF.
又
∵∠B = ∠C，
∴∠C = ∠CDF.
∴CE//BF.
∴∠E = ∠F.
“如果①③，那么②”是真命题. 证明如下：
∵AB//CD，
∴∠B = ∠CDF.
∵∠E = ∠F，
∴CE//BF.
∴∠C = ∠CDF.
∴∠B = ∠C.
“如果②③，那么①”是真命题. 证明如下：
∵∠E = ∠F，
∴CE//BF.
∴∠C = ∠CDF.
又
∵∠B = ∠C，
∴∠B = ∠CDF.
∴AB//CD.

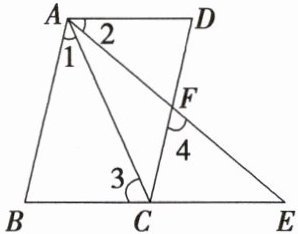
14. 如图，已知$AD// BE$，点$C$是$BE$上一点，连接$AB$，$AC$，$DC$，$AE$，$AE$与$CD$交于点$F$，$\angle1=\angle2$，$\angle3=\angle4$，求证：$AB// CD$.

答案： 证明：
∵AD//BE，
∴∠3 = ∠CAD.
∵∠3 = ∠4，
∴∠4 = ∠CAD.
∵∠1 = ∠2，
∴∠1 + ∠CAE = ∠2 + ∠CAE，
即∠BAE = ∠CAD.
∴∠4 = ∠BAE.
∴AB//CD.

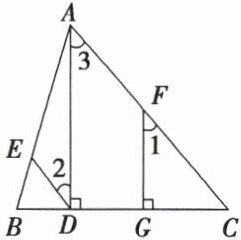
15. 如图，已知$AD\perp BC$，$FG\perp BC$，垂足分别为$D$，$G$，且$\angle1=\angle2$，猜想$\angle BDE$与$\angle C$有怎样的大小关系，试说明理由.

答案： 解：∠BDE = ∠C. 理由如下：
∵AD⊥BC，FG⊥BC，
∴∠ADC = ∠FGC = 90°.
∴AD//FG.
∴∠3 = ∠1.
又
∵∠1 = ∠2，
∴∠3 = ∠2.
∴ED//AC.
∴∠BDE = ∠C.