《2025年金考卷特快专递高中数学》

19.（12分）某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异，经过大量调查，得到如下的患病者和未患病者该指标的频率分布直方图：
　　
　　
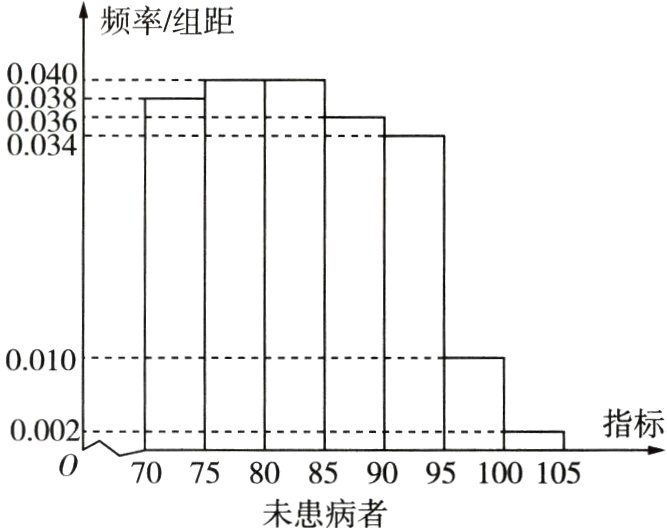
利用该指标制定一个检测标准，需要确定临界值$c$，将该指标大于$c$的人判定为阳性，小于或等于$c$的人判定为阴性. 此检测标准的漏诊率是将患病者判定为阴性的概率，记为$p(c)$；误诊率是将未患病者判定为阳性的概率，记为$q(c)$. 假设数据在组内均匀分布. 以事件发生的频率作为相应事件发生的概率.
(1)当漏诊率$p(c)=0.5\%$时，求临界值$c$和误诊率$q(c)$；
(2)设函数$f(c)=p(c)+q(c)$. 当$c\in[95,105]$时，求$f(c)$的解析式，并求$f(c)$在区间$[95,105]$的最小值.

答案：
19.频率分布直方图+样本估计总体+函数的解析式及最值(理性思维、数学应用、数学探索)
解题思路
(1)从频率分布直方图中获取相关数据,从而根据已知条件建立方程求出c的值,进而求出q(c);
(2)分95≤c≤100,100 ＜ c≤105两种情况分别求出p(c),q(c),再求出f(c),从而根据函数的单调性求结果.
解:
(1)第1步:求c的值
由题图知(100 - 95)×0.002 = 1% ＞ 0.5%,所以95 ＜ c ＜ 100,
设X为患病者的该指标,
则p(c)=P(X≤c)=(c - 95)×0.002 = 0.5%,(题眼)(从频率分布直方图中正确读取相关数据是求解问题的关键)
解得c = 97.5. (2分)
第2步:求q(c)
设Y为未患病者的该指标,
则q(c)=P(Y ＞ c)=(100 - 97.5)×0.01 + 5×0.002 = 0.035 = 3.5%. (4分)
(2)第1步:求函数f(c)的解析式
当95≤c≤100时,(提醒:注意分类讨论思想的应用)
p(c)=(c - 95)×0.002 = 0.002c - 0.19,
q(c)=(100 - c)×0.01 + 5×0.002 = - 0.01c + 1.01,
所以f(c)=p(c)+q(c)= - 0.008c + 0.82; (6分)
当100 ＜ c≤105时,
p(c)=5×0.002 + (c - 100)×0.012 = 0.012c - 1.19,
q(c)=(105 - c)×0.002 = - 0.002c + 0.21,
所以f(c)=p(c)+q(c)=0.01c - 0.98. (8分)
综上所述,f(c)=$\begin{cases}-0.008c + 0.82,95\leq c\leq100\\0.01c - 0.98,100 ＜ c\leq105\end{cases}$. (10分)
第2步:根据一次函数的单调性求最小值
由一次函数的单调性知,函数f(c)在[95,100]上单调递减,在(100,105]上单调递增,(提示:对于一次函数y = kx + b(k≠0),当k ＞ 0时,函数单调递增;当k ＜ 0时,函数单调递减)
作出f(c)在区间[95,105]上的大致图象(略),可得f(c)在区间[95,105]的最小值f(c)min=f
(100)= - 0.008×100 + 0.82 = 0.02. (12分)
考情速递 科学设置情境,探索数学学科应用价值 本题属于生活实践情境和探索创新情境融合试题,第
(1)问通过求临界值让学生切身感受检测标准是如何制定的,通过确定检测标准的临界值,使“漏诊率”和“误诊率”达到一种合理平衡,不要一个很高,另一个很低;第
(2)问通过分段函数考查利用函数的单调性求最值和数形结合思想.本题设计的问题具有现实意义,也具备研究价值.本题立意很好,比较新颖.

20. (12分)如图，三棱锥A - BCD中，DA = DB = DC，BD⊥CD，∠ADB = ∠ADC = 60°，E为BC的中点.
(1)证明：BC⊥DA；
(2)点F满足$\overrightarrow{EF}=\overrightarrow{DA}$，求二面角D - AB - F的正弦值.
　　　　　　　　　　　

答案：
20. 线线垂直 + 二面角的正弦值(理性思维)
解:
(1)第1步:作辅助线,证DE⊥BC,AE⊥BC
连接DE,AE,
因为DC = DB,且E为BC的中点,所以DE⊥BC. (1分)
因为∠ADB = ∠ADC = 60°,DA = DA,DC = DB,
所以△ADB≌△ADC(SAS). (2分)
可得AC = AB,故AE⊥BC. (3分)
第2步:证BC⊥平面ADE
因为DE∩AE = E,DE,AE⊂平面ADE,所以BC⊥平面ADE. (4分)
第3步:证BC⊥DA
又DA⊂平面ADE,所以BC⊥DA. (5分)
(2)解法一(空间向量法) 第1步:证ED,EB,EA两两垂直
由
(1)知,DE⊥BC,
AE⊥BC.
不妨设DA = DB = DC = 2,因为∠ADB = ∠ADC = 60°,所以AB = AC = 2.
由题可知△DBC为等腰直角三角形,故DE = EB = EC = $\sqrt{2}$. (6分)
因为AE⊥BC,所以AE = $\sqrt{AB^{2}-EB^{2}}=\sqrt{2}$.
在△ADE中,AE² + ED² = AD²,所以AE⊥ED. (提醒:要先证ED,EB,EA两两垂直,才能建系) (7分)
第2步:建系,写出相关坐标
以E为坐标原点,ED所在直线为x轴,EB所在直线为y轴,EA所在直线为z轴建立空间直角坐标系,
如图1,则D($\sqrt{2}$,0,0),B(0,$\sqrt{2}$,0),A(0,0,$\sqrt{2}$),$\overrightarrow{DA}=(-\sqrt{2},0,\sqrt{2})$,$\overrightarrow{BA}=(0,-\sqrt{2},\sqrt{2})$.
设F($x_{F}$,$y_{F}$,$z_{F}$),因为$\overrightarrow{EF}=\overrightarrow{DA}$,所以($x_{F}$,$y_{F}$,$z_{F}$) = (-$\sqrt{2}$,0,$\sqrt{2}$),可得F(-$\sqrt{2}$,0,$\sqrt{2}$).(关键一步:通过向量相等推F的坐标)(速解:因为$\overrightarrow{EF}=\overrightarrow{DA}$,所以四边形EDAF为平行四边形,可得F的坐标)
所以$\overrightarrow{FA}=(\sqrt{2},0,0)$. (8分)
第3步:分别求平面DAB、平面ABF的法向量
设平面DAB的法向量为$\boldsymbol{m}=(x_{1},y_{1},z_{1})$,
则$\begin{cases}\overrightarrow{DA}\cdot\boldsymbol{m}=0\\\overrightarrow{BA}\cdot\boldsymbol{m}=0\end{cases}$,即$\begin{cases}-\sqrt{2}x_{1}+\sqrt{2}z_{1} = 0\\-\sqrt{2}y_{1}+\sqrt{2}z_{1} = 0\end{cases}$,取$x_{1} = 1$,则$y_{1} = z_{1} = 1$,$\boldsymbol{m}=(1,1,1)$. (9分)
设平面ABF的法向量为$\boldsymbol{n}=(x_{2},y_{2},z_{2})$,
则$\begin{cases}\overrightarrow{FA}\cdot\boldsymbol{n}=0\\\overrightarrow{BA}\cdot\boldsymbol{n}=0\end{cases}$,即$\begin{cases}\sqrt{2}x_{2} = 0\\-\sqrt{2}y_{2}+\sqrt{2}z_{2} = 0\end{cases}$,得$x_{2} = 0$,取$y_{2} = 1$,则$z_{2} = 1$,$\boldsymbol{n}=(0,1,1)$. (10分)
第4步:求二面角D - AB - F的正弦值
所以$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle=\frac{\boldsymbol{m}\cdot\boldsymbol{n}}{\vert\boldsymbol{m}\vert\cdot\vert\boldsymbol{n}\vert}=\frac{2}{\sqrt{3}\times\sqrt{2}}=\frac{\sqrt{6}}{3}$. (注意:题目问的是正弦值,最后要记得转化) (11分)
记二面角D - AB - F的大小为θ,则$\sin\theta=\sqrt{1 - \cos^{2}\langle\boldsymbol{m},\boldsymbol{n}\rangle}=\sqrt{1 - (\frac{\sqrt{6}}{3})^{2}}=\frac{\sqrt{3}}{3}$,
故二面角D - AB - F的正弦值为$\frac{\sqrt{3}}{3}$. (12分)
解法二(综合几何法) 如图2,构造二面角D - AB - F的平面角.设DE = 1,由题设可得BC = 2,AF = DE = 1,EF = DA = AC = AB = DB = $\sqrt{2}$.
由
(1)可得BC⊥平面ADEF,故BC⊥EF,∠BEF = 90°.
因此BF = $\sqrt{BE^{2}+EF^{2}}=\sqrt{3}$,所以AB² + AF² = BF²,
故AB⊥AF.
在△ABC中可得AE = 1,所以AE² + DE² = AD²,AE⊥DE,即∠AED = 90°.又可得∠AEF = 45°,所以∠DEF = 135°.
设AB中点为H,BF中点为K,连接DH,KH,
则DH⊥AB,KH⊥AB,所以∠KHD为二面角D - AB - F的平面角. (9分)
连接DF,由DE = 1,EF = $\sqrt{2}$,∠DEF = 135°,可得DF² = 5,则DB² + BF² = DF²,所以DB⊥BF,即∠DBF = 90°.
连接DK,则DK² = DB² + BK² = $\frac{11}{4}$.
由DH = $\sqrt{DB^{2}-(\frac{AB}{2})^{2}}=\frac{\sqrt{6}}{2}$,KH = $\frac{1}{2}AF=\frac{1}{2}$可得$\cos\angle DHK=\frac{DH^{2}+HK^{2}-DK^{2}}{2\times DH\times HK}=-\frac{\sqrt{6}}{3}$.
记二面角D - AB - F的大小为θ,则$\sin\theta=\frac{\sqrt{3}}{3}$,
因此二面角D - AB - F的正弦值为$\frac{\sqrt{3}}{3}$. (12分)
易错警示 本题中求二面角的正弦值的易错点:一是使用向量法前应注意证明相交于一点的三条直线两两垂直;二是向量夹角公式求出来的是两平面法向量夹角的余弦值,还需转化为二面角的正弦值.