《2025年金考卷特快专递高中数学》

1. 函数$y = \log_{2}x$的定义域为________.

答案： $(0,+\infty)$

2. 直线$x - y + 1 = 0$的倾斜角为________.

答案： $\frac{\pi}{4}$

3. 已知复数$z$满足$\frac{z}{1 + i} = i$,则$\overline{z} = $________.

答案： $-1 - i$

4. $(x - 1)^{6}$的展开式中$x^{4}$的系数为________.

答案： 15

5. 在$\triangle ABC$中,$BC = 2,A = \frac{\pi}{3},B = \frac{\pi}{4}$,则$AB = $________.

答案： $\frac{3\sqrt{2}+\sqrt{6}}{3}$

6. 已知$ab = 1$,则$4a^{2} + 9b^{2}$的最小值为________.

答案： 12

7. 已知数列$\{ a_{n}\}$的前$n$项和为$S_{n}$,且$a_{n} = n + c,S_{7} ＜ 0$,则$c$的取值范围为________.

答案： $c ＜ - 4$

8. 已知三角形三条边长分别为5,6,7,则以边长为6的两个顶点为焦点,过另外一个顶点的双曲线的离心率为________.

答案： 3

9. 已知函数$f(x) = x^{2},g(x) = \begin{cases}f(x),x\geq0\\ -f( -x),x ＜ 0\end{cases}$,若$g(x)$满足$g(x)\leq2 - x$,则$x$的取值范围为________.

答案： $x\leqslant1$

12. 已知$a_{1}=2,a_{2}=4,a_{3}=8,a_{4}=16$,对任意的$b_{1},b_{2},b_{3},b_{4}\in\mathbf{R}$,满足$\{ a_{i}+a_{j}|1\leqslant i ＜ j\leqslant4\} =\{ b_{i}+b_{j}|1\leqslant i ＜ j \leqslant 4\}$,求有序数列$\{ b_{1},b_{2},b_{3},b_{4}\}$有__________对.

答案： 48 排列组合 由题意可知$\{ a_{i}+a_{j}|1\leqslant i ＜ j\leqslant 4\} = \{ 6,10,12,18,20,24\}$，不妨设$b_{1}\leqslant b_{2}\leqslant b_{3}\leqslant b_{4}$，则存在两种情况：一是$b_{1}+b_{2}\leqslant b_{1}+b_{3}\leqslant b_{2}+b_{3}\leqslant b_{1}+b_{4}\leqslant b_{2}+b_{4}\leqslant b_{3}+b_{4}$，此时$b_{1}+b_{2}=6$，$b_{1}+b_{3}=10$，$b_{2}+b_{3}=12$，$b_{1}+b_{4}=18$，$b_{2}+b_{4}=20$，$b_{3}+b_{4}=24$，解得$b_{1}=2$，$b_{2}=4$，$b_{3}=8$，$b_{4}=16$，此时有序数列$\{ b_{1},b_{2},b_{3},b_{4}\}$有$A_{4}^{4}=24$（对）；（注：本题中所有$A_{4}^{4}$上海考生都换成$P_{4}^{4}$）二是$b_{1}+b_{2}\leqslant b_{1}+b_{3}\leqslant b_{1}+b_{4}\leqslant b_{2}+b_{3}\leqslant b_{2}+b_{4}\leqslant b_{3}+b_{4}$，此时$b_{1}+b_{2}=6$，$b_{1}+b_{3}=10$，$b_{1}+b_{4}=12$，$b_{2}+b_{3}=18$，$b_{2}+b_{4}=20$，$b_{3}+b_{4}=24$，解得$b_{1}=-1$，$b_{2}=7$，$b_{3}=11$，$b_{4}=13$，此时有序数列$\{ b_{1},b_{2},b_{3},b_{4}\}$有$A_{4}^{4}=24$（对）. 综上，有序数列$\{ b_{1},b_{2},b_{3},b_{4}\}$共有$2A_{4}^{4}=48$（对）.

10. (利用反三角函数表示角的大小,非上海地区考生不作要求)如图,已知四棱柱$ABCD - A_{1}B_{1}C_{1}D_{1}$,底面$ABCD$为平行四边形,$AA_{1} = 3,BD = 4$且$\overrightarrow{AB_{1}}\cdot\overrightarrow{BC}-\overrightarrow{AD_{1}}\cdot\overrightarrow{DC}=5$,则异面直线$AA_{1}$与$BD$的夹角为________.

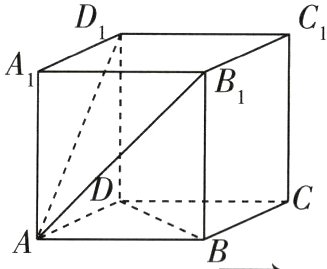
答案： $\arccos\frac{5}{12}$

11. 如图,正方形草地$ABCD$的边长为1.2,点$E$到$AB,AD$的距离均为0.2,点$F$到$BC,CD$的距离均为0.4,有个圆形通道经过$E,F$两点,且和$AD$有且仅有一个交点,则圆形通道的周长为________. ($\sqrt{2}\approx1.414$,结果精确到0.01)

答案： 2.73

13. 已知$a,b,c\in\mathbf{R},b ＞ c$,则下列不等式一定成立的是
A. $a + b^{2} ＞ a + c^{2}$
B. $a^{2}+b ＞ a^{2}+c$
C. $ab^{2} ＞ ac^{2}$
D. $a^{2}b ＞ a^{2}c$

答案： B 不等式的性质 通解 当$b ＞ c\geqslant 0$时，$b^{2}＞c^{2}$，当$c ＜ b\leqslant 0$时，$b^{2}＜c^{2}$，所以$a + b^{2}＞a + c^{2}$不一定成立，故A错误；
因为$b ＞ c$，$a^{2}\geqslant 0$，所以$a^{2}+b ＞ a^{2}+c$成立，故B正确；
当$a ＞ 0$，$c ＜ b\leqslant 0$时，$ab^{2}＜ac^{2}$，当$a ＜ 0$，$b ＞ c\geqslant 0$时，$ab^{2}＜ac^{2}$，当$a = 0$时，$ab^{2}=ac^{2}$，这三种情况下$ab^{2}＞ac^{2}$都不成立，故C错误；
当$a = 0$时，$a^{2}b ＞ a^{2}c$不成立，故D错误. 综上，选B.
光速解 令$a = 0$，$b = -1$，$c = -2$，分别代入选项A，B，C，D可知只有$a^{2}+b ＞ a^{2}+c$成立，故选B.

14. 已知空间中有两个不重合的平面$\alpha,\beta$和两条不重合的直线$m,n$,则下列说法中正确的是
A. 若$\alpha\perp\beta,m\perp\alpha,n\perp\beta$,则$m\perp n$
B. 若$\alpha\perp\beta,m\perp\alpha,m\perp n$,则$n\perp\beta$
C. 若$\alpha//\beta,m//\alpha,n//\beta$,则$m// n$
D. 若$\alpha//\beta,m//\alpha,m// n$,则$n//\beta$

答案： A 空间直线与平面的位置关系 若$\alpha\perp\beta$，$m\perp\alpha$，则$m//\beta$或$m\subset\beta$，又$n\perp\beta$，所以$m\perp n$，故A正确；
若$\alpha\perp\beta$，$m\perp\alpha$，则$m//\beta$或$m\subset\beta$，又$m\perp n$，则$n\subset\beta$或$n$与$\beta$斜交或$n\perp\beta$均有可能，故B错误；
若$\alpha//\beta$，$m//\alpha$，则$m\subset\beta$或$m//\beta$，又$n//\beta$，因此$m$和$n$的位置关系可能为平行、相交或异面，故C错误；
若$\alpha//\beta$，$m//\alpha$，$m// n$，则$n//\beta$或$n\subset\beta$，故D错误.
综上，选A.

15. 有四个礼盒,前三个里面分别仅装有中国结、记事本、笔袋,第四个礼盒里面上述三种礼品都装的有,现从中任选一个礼盒. 设事件$A$为“所选礼盒中有中国结”,事件$B$为“所选礼盒中有记事本”,事件$C$为“所选礼盒中有笔袋”,则下列说法中正确的是
A. 事件$A$与事件$B$互斥
B. 事件$A$与事件$B$相互独立
C. 事件$A$与事件$B\cup C$互斥
D. 事件$A$与事件$B\cap C$相互独立

答案： B 相互独立事件 + 互斥事件 由于第四个礼盒中既有中国结，又有记事本，若抽到第四个礼盒，则事件$A$和事件$B$就同时发生了，因此事件$A$与事件$B$不是互斥事件，故A错误；
由于$P(A)=\frac{1}{2}$，$P(B)=\frac{1}{2}$，$P(A\cap B)=\frac{1}{4}=P(A)\cdot P(B)$，因此事件$A$与事件$B$相互独立，故B正确；
由于第四个礼盒中既有中国结，又有记事本，还有笔袋，若抽到第四个礼盒，则事件$A$和事件$B\cup C$就同时发生了，因此事件$A$与事件$B\cup C$不是互斥事件，故C错误；
由于$P(A)=\frac{1}{2}$，$P(B\cap C)=\frac{1}{4}$，$P(A\cap B\cap C)=\frac{1}{4}\neq P(A)\cdot P(B\cap C)$，因此事件$A$与事件$B\cap C$不是相互独立的，故D错误.
综上，选B.
考情速递 强调概念理解·吃透教材 本题考查了相互独立事件、互斥事件的定义，突出了概率与统计部分概念、定义的地位，也考查了学生对知识的深刻理解，体现了“双新”背景下的评价要求.

16. 现定义如下:当$x\in(n,n + 1)(n\in\mathbf{N})$时,若$f(x + 1)=f'(x)$,则称$f(x)$为延展函数. 当$x\in(0,1)$时,$g(x)=\mathrm{e}^{x},h(x)=x^{10}$. 已知$g(x)$和$h(x)$均为延展函数,给出下列结论:①存在直线$y = kx + b$ $(k,b\in\mathbf{R}$且$k,b\neq0)$与$y = g(x)$的图象有无穷个交点;②存在直线$y = kx + b(k,b\in\mathbf{R}$且$k,b\neq0)$与$y = h(x)$的图象有无穷个交点. 则下列说法正确的是
A. ①②都成立
B. ①②都不成立
C. ①成立②不成立
D. ①不成立②成立

答案：
D 新定义 + 函数的图象与性质 当$x\in(0,1)$时，$g(x + 1)=g'(x)=e^{x}$，则$x\in(1,2)$时，$g(x)=e^{x - 1}$，$\cdots$，$x\in(n,n + 1)(n\in\mathbf{N})$时，$g(x)=e^{x - n}$，（提示：从特殊到一般）画出函数$y = g(x)$，$x\in(n,n + 1)(n\in\mathbf{N})$的图象，如图a所示，此时，不存在直线$y = kx + b(k,b\in\mathbf{R}$且$k,b\neq0)$与$y = g(x)$的图象有无穷个交点，故①不成立；当$x\in(0,1)$时，$h(x + 1)=h'(x)=10x^{9}$，则$x\in(1,2)$时，$h(x)=10(x - 1)^{9}$，$\cdots$，$x\in(9,10)$时，$h(x)=A_{10}^{9}(x - 9)$，$h(x)$的示意图如图b所示，当$n = 9$时，$h(x)=A_{10}^{9}(x - 9)$，$x\in(9,10)$，令$y = 10!(x - 9)$，则该直线与$h(x)$在$(9,10)$上的图象重合，此时这一段有无穷个交点，故②成立.
　　　 　　
综上，选D.