《2025年通城学典非常课课通九年级数学下册苏科版江苏专版》

1.（2024·徐州模拟）如图，在Rt△ABC中，∠C = 90°，AC = 6，BC = 2.点P在边AC上，从点A向点C移动，点Q在边CB上，从点C向点B移动.若点P、Q均以每秒1个单位长度的速度同时出发，且当一点移动到终点时，另一点也随之停止.连接PQ，则线段PQ长的最小值是（ ）

A. 2√7
B. 3√3
C. 2√5
D. 3√2

答案： C

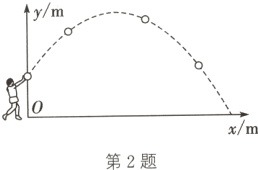
2. 如图，一男生推铅球，铅球行进高度y（m）是水平距离x（m）的二次函数，即铅球飞行轨迹是一条抛物线.该男生推铅球出手时，铅球的高度为1.6 m；铅球飞行至水平距离4 m时，铅球的高度为4 m，铅球落地时水平距离为8 m.有下列结论：① 铅球飞行至水平距离3.5 m时，铅球到达最大高度，最大高度为4.05 m；② 当0≤x≤8时，y与x之间的函数表达式为y = -$\frac{1}{5}$x² + $\frac{7}{5}$x + $\frac{8}{5}$；③ 铅球从出手到飞行至最高点的水平距离与从最高点运动至落地的水平距离相等.其中，正确的个数是（ ）

A. 3
B. 2
C. 1
D. 0

答案： B

3.（2024·保德三模）“科教兴国，强国有我”.某中学在科技实验活动中，设计制作了“水火箭”升空实验，已知“水火箭”的升空高度h（m）与飞行时间t（s）满足函数表达式h = at² + bt + 1（a，b为常数，且a≠0）.已知“水火箭”飞行3 s和飞行9 s时的升空高度相同，飞行8 s时的升空高度为33 m，则“水火箭”升空的最大高度为（ ）
A. 33 m
B. 36 m
C. 37 m
D. 40 m

答案： C

4.（2024·芜湖段考）某农场拟建两间矩形饲养室，一面靠现有墙（墙足够长），中间用一道墙隔开，并在如图所示的三处各留1 m宽的门.已知计划中的材料可建墙体（不包括门）总长为27 m，则能建成的饲养室面积最大为________m².

答案： 75

5.（2024·烟台）每年5月的第三个星期日为全国助残日，今年的主题是“科技助残，共享美好生活”.某公司新研发了一批便携式轮椅，计划在该月销售.根据市场调查，每辆轮椅盈利200元时，每天可售出60辆；单价每降低10元，每天可多售出4辆.公司决定在成本不变的情况下降价销售，但每辆轮椅的利润不低于180元.设每辆轮椅降价x元，每天的销售利润为y元.
（1）求y与x之间的函数表达式.当每辆轮椅降价多少元时，每天的销售利润最大？最大利润为多少元？
（2）全国助残日当天，公司共获得销售利润12 160元，则这天售出了多少辆轮椅？

答案： （1）由题意，得$y=(200 - x)(60 + 4\times\frac{x}{10})=-0.4x^{2}+20x + 12000=-0.4(x^{2}-50x + 625)+12250=-0.4(x - 25)^{2}+12250$.$\because$易得$200 - x\geqslant180$，$\therefore x\leqslant20$.$\because -0.4\lt0$，$\therefore$当$x\lt25$时，$y$随$x$的增大而增大.$\therefore$当$x = 20$时，$y$取最大值，最大值为$-0.4\times(20 - 25)^{2}+12250 = 12240$.$\therefore y$与$x$之间的函数表达式为$y=-0.4x^{2}+20x + 12000$；当每辆轮椅降价20元时，每天的销售利润最大，最大利润为12240元 （2）根据题意，得$-0.4(x - 25)^{2}+12250 = 12160$，解得$x_{1}=40$（不合题意，舍去），$x_{2}=10$.$\therefore$这天售出了$60 + 4\times\frac{10}{10}=64$（辆）轮椅