《2025年通城学典非常课课通九年级数学下册苏科版江苏专版》

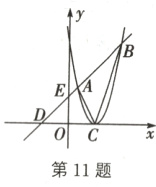
11. 如图，抛物线$y = x^{2}-(m + 3)x + 9$的顶点$C$在$x$轴的正半轴上，直线$y = x + 3$与抛物线交于$A$、$B$两点（点$A$在点$B$的左侧），与$x$轴、$y$轴分别交于$D$、$E$两点.
（1）求$m$的值；
（2）求$A$、$B$两点的坐标；
（3）若$P(a,b)(-3 ＜ a ＜ 1)$是抛物线上一点，当$\triangle PAB$的面积是$\triangle ABC$面积的2倍时，求$a$、$b$的值.
　　　　　　　　　　　

答案：
(1) 抛物线$y = x^{2}-(m + 3)x + 9$的顶点$C$的坐标为$(\frac{m + 3}{2},9-\frac{(m + 3)^{2}}{4})$.
∵ 顶点$C$在$x$轴的正半轴上，
∴ $\begin{cases}\frac{m + 3}{2}＞0\\9-\frac{(m + 3)^{2}}{4}=0\end{cases}$，解得$\begin{cases}m＞-3\\m = 3或m = - 9\end{cases}$.
∴ $m = 3$
(2)
∵ $m = 3$，
∴ 抛物线对应的函数表达式为$y = x^{2}-6x + 9$. 根据题意，得$\begin{cases}y = x + 3\\y = x^{2}-6x + 9\end{cases}$，解得$\begin{cases}x_{1}=1\\y_{1}=4\end{cases}$，$\begin{cases}x_{2}=6\\y_{2}=9\end{cases}$.
∵ 点$A$在点$B$的左侧，
∴ 点$A$的坐标为$(1,4)$，点$B$的坐标为$(6,9)$
(3) 连接$CE$，过点$P$作$PM\perp AB$于点$M$，$PN\perp x$轴于点$N$，交$BD$于点$F$. 根据题意，易得$OE = OC = OD = 3$，$CE\perp AB$.
∴ 在$Rt\triangle EOC$中，$CE=\sqrt{3^{2}+3^{2}}=3\sqrt{2}$.
∵ $S_{\triangle PAB}=2S_{\triangle ABC}$，
∴ $\frac{1}{2}AB\cdot PM = 2\times\frac{1}{2}AB\cdot CE$.
∴ $PM = 2CE = 6\sqrt{2}$. 由题意，易得$\triangle PMF$是等腰直角三角形，
∴ $PF=\sqrt{PM^{2}+MF^{2}}=\sqrt{2}PM = 12$.
∵ 点$F$在直线$y = x + 3$上，点$P$的坐标为$(a,b)$，
∴ 点$F$的坐标为$(a,a + 3)$.
∵ $-3＜a＜1$，
∴ $a + 3＞0$.
∴ $PF = PN - FN = b-(a + 3)=b - a - 3 = 12$，即$b = a + 15$①.
∵ 点$P(a,b)$在抛物线$y = x^{2}-6x + 9$上，
∴ $a^{2}-6a + 9 = b$②. 由①②，可得$a^{2}-6a + 9 = a + 15$，解得$a_{1}=\frac{7+\sqrt{73}}{2}$，$a_{2}=\frac{7-\sqrt{73}}{2}$. 又
∵ $-3＜a＜1$，
∴ $a=\frac{7-\sqrt{73}}{2}$.
∴ $b=\frac{7-\sqrt{73}}{2}+15=\frac{37-\sqrt{73}}{2}$

12.（2024·启东期中）已知二次函数$y = x^{2}+2(m - 2)x - m + 2$的图像与$x$轴最多有一个交点.若$y = m^{2}-2tm - 3$的最小值为3，则$t$的值为（ ）
A. $-\frac{1}{2}$
B. $\frac{3}{2}$或$-\frac{3}{2}$
C. $-\frac{5}{2}$或$-\frac{3}{2}$
D. $-\frac{5}{2}$

答案： D 解析：根据题意，得一元二次方程$x^{2}+2(m - 2)x - m + 2 = 0$最多只有一个解，
∴ $[2(m - 2)]^{2}-4(2 - m)\leqslant0$.
∴ $1\leqslant m\leqslant2$.
∵ $y = m^{2}-2tm - 3=(m - t)^{2}-t^{2}-3$，
∴ $y$关于$m$的函数图像的对称轴为直线$m = t$. 分三种情况：① 当$t\geqslant2$时，
∵ $1\leqslant m\leqslant2$，
∴ 自变量$m$对应函数图像的点在对称轴上或对称轴的左侧.
∵ $a = 1＞0$，
∴ 在对称轴的左侧$y$随$m$的增大而减小.
∴ 当$m$取最大值2时，$y$取得最小值$2^{2}-2\times2\times t - 3 = 1 - 4t$.
∵ 这个最小值为3，
∴ $1 - 4t = 3$，解得$t = -\frac{1}{2}$(不合题意，舍去). ② 当$t\leqslant1$时，
∵ $1\leqslant m\leqslant2$，
∴ 自变量$m$对应函数图像的点在对称轴上或对称轴的右侧.
∵ $a = 1＞0$，
∴ 在对称轴的右侧$y$随$m$的增大而增大.
∴ 当$m$取最小值1时，$y$取得最小值$1^{2}-2\times1\times t - 3 = - 2 - 2t$.
∵ 这个最小值为3，
∴ $-2 - 2t = 3$，解得$t = -\frac{5}{2}$，符合题意. ③ 当$1＜t＜2$时，
∵ $1\leqslant m\leqslant2$，
∴ 当$m = t$时，$y$取得最小值$t^{2}-2t^{2}-3=-t^{2}-3$.
∵ 这个最小值为3，
∴ $-t^{2}-3 = 3$，此方程无解. 综上所述，$t$的值为$-\frac{5}{2}$.

13.（2024·宿城一模）在平面直角坐标系中，点$M$、$N$的坐标分别为$(-1,2)$、$(2,1)$.若抛物线$y = ax^{2}-x + 2$（$a\neq0$）与线段$MN$有两个不同的交点，则$a$的取值范围是__________.

答案： $\frac{1}{4}\leqslant a＜\frac{1}{3}$或$a\leqslant - 1$

14.（南通模拟）已知二次函数$y = x^{2}-4x + 3a + 2$（$a$为常数）.
（1）请写出该二次函数的三条性质；
（2）在同一平面直角坐标系中，若该二次函数的图像在$x\leq4$的部分与一次函数$y = 2x - 1$的图像有两个交点，求$a$的取值范围.

答案：
(1)
∵ $y = x^{2}-4x + 3a + 2=(x - 2)^{2}+3a - 2$，
∴ 该二次函数具有以下性质(答案不唯一)：① 它的图像开口向上；② 它的图像的对称轴为直线$x = 2$；③ 当$x＜2$时，$y$随$x$的增大而减小
(2) 设两个函数图像在$x\leqslant4$的部分的两个交点坐标为$(x_{1},y_{1})$、$(x_{2},y_{2})$，则$x_{1}\leqslant4$，$x_{2}\leqslant4$，且方程组$\begin{cases}y = x^{2}-4x + 3a + 2①\\y = 2x - 1②\end{cases}$的解为$\begin{cases}x = x_{1}\\y = y_{1}\end{cases}$，$\begin{cases}x = x_{2}\\y = y_{2}\end{cases}$. 把②代入①，得$2x - 1 = x^{2}-4x + 3a + 2$，
∴ $x^{2}-6x + 3a + 3 = 0$.
∴ $(-6)^{2}-4\times1\times(3a + 3)＞0$，解得$a＜2$③.
∵ $x_{1}\leqslant4$，$x_{2}\leqslant4$，
∴ $x_{1}-4\leqslant0$，$x_{2}-4\leqslant0$.
∴ $\begin{cases}x_{1}-4 + x_{2}-4 = x_{1}+x_{2}-8\leqslant0\\(x_{1}-4)(x_{2}-4)=x_{1}x_{2}-4(x_{1}+x_{2})+16\geqslant0\end{cases}$. 由根与系数的关系，得$x_{1}+x_{2}=6$，$x_{1}x_{2}=3a + 3$.
∴ $\begin{cases}6 - 8\leqslant0\\3a + 3-24 + 16\geqslant0\end{cases}$，解得$a\geqslant\frac{5}{3}$④. 由③④，可知$a$的取值范围是$\frac{5}{3}\leqslant a＜2$