《2025年通城学典非常课课通九年级数学下册苏科版江苏专版》

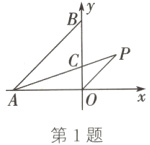
1.（2024·凉州二模）如图，在平面直角坐标系中，点A、B分别在x轴的负半轴和y轴的正半轴上，点C在OB上，OC：BC = 1：2，连接AC，过点O作OP//AB，交AC的延长线于点P.若P(1,1)，则tan∠OAP的值是（ ）

A. $\frac{\sqrt{3}}{3}$
B. $\frac{\sqrt{2}}{2}$
C. $\frac{1}{3}$
D. 3

答案： C

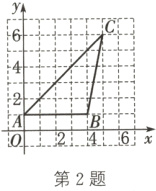
2.（2023·益阳）如图，在平面直角坐标系中，有三点A(0,1)、B(4,1)、C(5,6)，则sin∠BAC的值为（ ）

A. $\frac{1}{2}$
B. $\frac{\sqrt{13}}{5}$
C. $\frac{\sqrt{2}}{2}$
D. $\frac{\sqrt{3}}{2}$

答案： C

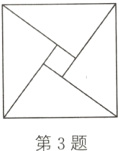
3.（2023·包头）如图所示为源于我国汉代数学家赵爽的弦图，它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为α，则cosα的值为（ ）

A. $\frac{3}{4}$
B. $\frac{4}{3}$
C. $\frac{3}{5}$
D. $\frac{4}{5}$

答案： D

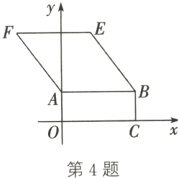
4. 如图，在平面直角坐标系中，矩形OABC的顶点B的坐标为(10,4)，点A在y轴上，点C在x轴上，四边形ABEF是菱形，且tan∠ABE = $\frac{4}{3}$.若直线l把矩形OABC和菱形ABEF组成的图形的面积分成相等的两部分，则直线l对应的函数表达式为（ ）

A. y = 3x
B. y = -$\frac{3}{4}$x + $\frac{15}{2}$
C. y = -2x + 11
D. y = -2x + 12

答案：
D 解析：如图，过点E作EG⊥AB于点G，连接OB、AC，交于点M，连接AE、BF，交于点N. 根据中心对称的性质，易知直线MN即为符合条件的直线l.
∵点B的坐标为(10,4)，
∴OC = 10，BC = 4.
∵四边形OABC是矩形，
∴AB = OC = 10，OA = BC = 4，M为OB的中点.
∴易得点M的坐标为(5,2).
∵四边形ABEF为菱形，
∴BE = AB = 10，N为AE的中点. 在Rt△BEG中，
∵tan∠ABE = $\frac{4}{3}$，
∴$\frac{EG}{BG}=\frac{4}{3}$. 设EG = 4k(k＞0)，则BG = 3k.
∴BE = $\sqrt{EG^{2}+BG^{2}}$ = 5k.
∴5k = 10.
∴k = 2.
∴EG = 8，BG = 6.
∴AG = AB - BG = 10 - 6 = 4.
∴易得点E的坐标为(4,12).
∵OA = 4，
∴点A的坐标为(0,4).
∵N为AE的中点，
∴易得点N的坐标为(2,8). 设直线l对应的函数表达式为y = ax + b. 把M(5,2)、N(2,8)代入，得$\begin{cases}5a + b = 2\\2a + b = 8\end{cases}$，解得$\begin{cases}a = - 2\\b = 12\end{cases}$.
∴直线l对应的函数表达式为y = - 2x + 12.

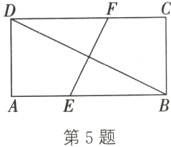
5.（2024·常州）如图，在矩形ABCD中，对角线BD的垂直平分线分别交边AB、CD于点E、F.如果AD = 8，BE = 10，那么tan∠ABD = ______.

答案： $\frac{1}{2}$

6. 在△ABC中，∠C = 90°，a、b、c分别为∠A、∠B、∠C的对边.若b² = ac，则sinA的值为______.

答案： $\frac{\sqrt{5}-1}{2}$ 解析：
∵∠C = 90°，
∴$c^{2}=a^{2}+b^{2}$. 又
∵$b^{2}=ac$，
∴$c^{2}=a^{2}+ac$，即$a^{2}+ac - c^{2}=0$，解得$a = \frac{\sqrt{5}-1}{2}c$或$a = \frac{-\sqrt{5}-1}{2}c$(不合题意，舍去).
∵∠C = 90°，
∴sin A = $\frac{a}{c}=\frac{\frac{\sqrt{5}-1}{2}c}{c}=\frac{\sqrt{5}-1}{2}$.

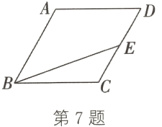
7.（2024·无锡改编）如图，在菱形ABCD中，∠ABC = 60°，E是CD的中点，则sin∠EBC的值为______.

答案：
$\frac{\sqrt{21}}{14}$ 解析：如图，过点E作EH⊥BC，交BC的延长线于点H.
∵四边形ABCD是菱形，
∴BC = CD，AB//CD.
∴∠ABC = ∠ECH = 60°. 设BC = CD = 4k.
∵E是CD的中点，
∴CE = $\frac{1}{2}CD=\frac{1}{2}\times4k = 2k$.
∵∠EHC = 90°，
∴∠CEH = 90° - ∠ECH = 90° - 60° = 30°.
∴易得CH = $\frac{1}{2}CE=\frac{1}{2}\times2k = k$.
∴BH = BC + CH = 4k + k = 5k.
∴在Rt△CEH中，由勾股定理，得EH = $\sqrt{CE^{2}-CH^{2}}=\sqrt{(2k)^{2}-k^{2}}=\sqrt{3}k$.
∵∠BHE = 90°，
∴在Rt△BHE中，由勾股定理，得BE = $\sqrt{EH^{2}+BH^{2}}=\sqrt{(\sqrt{3}k)^{2}+(5k)^{2}} = 2\sqrt{7}k$.
∴sin∠EBC = $\frac{EH}{BE}=\frac{\sqrt{3}k}{2\sqrt{7}k}=\frac{\sqrt{3}\times\sqrt{7}}{2\sqrt{7}\times\sqrt{7}}=\frac{\sqrt{21}}{14}$.

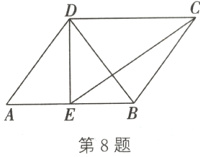
8.（2024·姑苏一模）如图，在□ABCD中，BD = AD，E为边AB的中点，连接DE.若sinA = $\frac{4}{5}$，则tan∠BCE的值为______.

答案：
$\frac{6}{17}$ 解析：如图，过点B作BH⊥CE于点H.
∵BD = AD，E为边AB的中点，
∴DE⊥AB.
∴∠AED = 90°. 在Rt△AED中，
∵sin A = $\frac{4}{5}$，
∴$\frac{DE}{AD}=\frac{4}{5}$. 设DE = 4x，则AD = 5x.
∴AE = $\sqrt{AD^{2}-DE^{2}} = 3x$.
∴BE = AE = 3x.
∵四边形ABCD是平行四边形，
∴CD = AB = 3x + 3x = 6x，BC = AD = 5x，AB//DC.
∴∠EDC = ∠AED = 90°.
∴CE = $\sqrt{DE^{2}+CD^{2}} = 2\sqrt{13}x$.
∵$S_{\triangle BEC}=\frac{1}{2}CE\cdot BH=\frac{1}{2}BE\cdot DE$，
∴$\frac{1}{2}\times2\sqrt{13}x\cdot BH=\frac{1}{2}\times3x\times4x$，解得BH = $\frac{6\sqrt{13}}{13}x$.
∵∠BHC = 90°，
∴CH = $\sqrt{BC^{2}-BH^{2}}=\frac{17\sqrt{13}}{13}x$.
∴tan∠BCE = $\frac{BH}{CH}=\frac{6}{17}$.

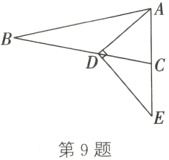
9.（2024·深圳）如图，在△ABC中，AB = BC，tanB = $\frac{5}{12}$，D为BC上一点，且满足$\frac{BD}{CD}$ = $\frac{8}{5}$，连接AD，过点D作DE⊥AD，交AC的延长线于点E，则$\frac{CE}{AC}$ = ______.

答案：
$\frac{20}{21}$ 解析：如图，分别过点A、C作AH⊥CB于点H、CF⊥AD于点F，则∠AHB = ∠CFD = 90°.
∵$\frac{BD}{DC}=\frac{8}{5}$，
∴设BD = 8a，则CD = 5a.
∴AB = BC = BD + CD = 13a.
∵∠AHB = 90°，tan B = $\frac{5}{12}$，
∴$\frac{AH}{BH}=\frac{5}{12}$.
∵AB = 13a，
∴易得AH = 5a，BH = 12a.
∴DH = BH - BD = 4a.
∴在Rt△ADH中，AD = $\sqrt{AH^{2}+DH^{2}}=\sqrt{41}a$.
∵cos∠ADH = $\frac{DH}{AD}$，cos∠CDF = $\frac{DF}{CD}$，
∴$\frac{DH}{AD}=\frac{DF}{CD}$.
∴$\frac{4a}{\sqrt{41}a}=\frac{DF}{5a}$.
∴DF = $\frac{20\sqrt{41}}{41}a$.
∴AF = AD - DF = $\frac{21\sqrt{41}}{41}a$.
∵易知CF//DE，
∴$\frac{CE}{AC}=\frac{DF}{AF}=\frac{20}{21}$.