《2025年通城学典非常课课通九年级数学下册苏科版江苏专版》

7.（2024·三亚一模）如图，数学兴趣小组为了测量河对岸的古树A、B之间的距离，他们在河边与AB平行的直线MN上取相距60 m的C、D两点，测得∠ACB = 15°，∠BCD = 120°，∠ADC = 30°.
（1）∠ACM = ________°，∠BCM = ________°；
（2）求河的宽度；
（3）求古树A、B之间的距离.

答案：

(1) 45 60
(2) 如图，过点A作AE⊥MN于点E. 设CE = x m，则DE = CE + CD = (x + 60)m.
∵∠ACB = 15°，∠BCD = 120°，
∴∠ACE = 180° - ∠ACB - ∠BCD = 45°. 在Rt△AEC中，AE = CE·tan45° = x m. 在Rt△ADE中，
∵tan∠ADE = AE/ED，
∴tan30° = x/(x + 60) = √3/3，解得x = 30√3 + 30. 经检验，x = 30√3 + 30是原分式方程的解，且符合题意.
∴AE = (30√3 + 30)m.
∴河的宽度为(30√3 + 30)m
(3) 如图，过点B作BF⊥MN于点F.
∵AB//MN，
∴∠ABF = ∠BFC = 90°.
∵∠AEF = ∠EFB = 90°，
∴四边形ABFE为矩形.
∴CE = AE = BF = (30√3 + 30)m，AB = EF.
∵∠BCD = 120°，
∴∠BCF = 180° - ∠BCD = 60°. 在Rt△BCF中，CF = BF/tan60° = (30√3 + 30)/√3 = (30 + 10√3)m.
∴AB = EF = CE - CF = 30√3 + 30 - (30 + 10√3) = 20√3(m).
∴古树A、B之间的距离为20√3 m

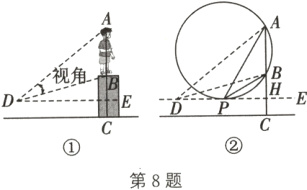
8.（2024·河南）如图①，塑像AB在底座BC上，点D是人眼所在的位置. 当点B高于人的水平视线DE时，由远及近看塑像，会在某处感觉看到的塑像最大，此时视角最大. 数学家研究发现：当经过A、B两点的圆与水平视线DE相切时（如图②），在切点P处感觉看到的塑像最大，此时∠APB为最大视角.
（1）请仅就图②的情形求证∠APB＞∠ADB.
（2）经测量，最大视角∠APB为30°，在点P处看塑像顶部点A的仰角∠APE为60°，点P到塑像的水平距离PH为6 m. 求塑像AB的高（精确到0.1 m，参考数据：$\sqrt{3}$≈1.73）.

答案：

(1) 如图，设AD与圆交于点M，连接BM.
∵∠AMB = ∠APB，∠AMB＞∠ADB，
∴∠APB＞∠ADB
(2) 在Rt△APH中，
∵∠AHP = 90°，∠APH = 60°，PH = 6 m，
∴AH = PH·tan60° = 6×√3 = 6√3(m).
∵∠APB = 30°，
∴∠BPH = ∠APH - ∠APB = 60° - 30° = 30°. 在Rt△BPH中，
∵∠BHP = 90°，∠BPH = 30°，PH = 6 m，
∴BH = PH·tan30° = 6×√3/3 = 2√3(m).
∴AB = AH - BH = 6√3 - 2√3 = 4√3≈4×1.73≈6.9(m).
∴塑像AB的高约为6.9 m

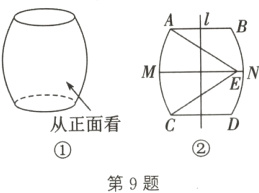
9.（2024·石家庄模拟）如图①所示为一张圆凳的造型，这张圆凳的上、下底面圆的直径都是30 cm，高为42.9 cm. 它被平行于上、下底面的平面所截得的横截面都是圆，小明画出了它的主视图，是由上、下底面圆的直径AB、CD以及$\overset{\frown}{AC}$、$\overset{\frown}{BD}$组成的轴对称图形，直线l为对称轴，M、N分别是$\overset{\frown}{AC}$、$\overset{\frown}{BD}$的中点，如图②，他又画出了$\overset{\frown}{AC}$所在的扇形并度量出扇形的圆心角∠AEC = 66°，发现并证明了点E在MN上. 请你继续计算MN的长（参考数据：sin66°≈$\frac{9}{10}$，cos66°≈$\frac{2}{5}$，tan66°≈$\frac{9}{4}$，sin33°≈$\frac{11}{20}$，cos33°≈$\frac{11}{13}$，tan33°≈$\frac{13}{20}$）.

答案：
如图，连接AC，交MN于点H，设直线l交MN于点Q.
∵M是AC的中点，点E在MN上，
∴∠AEM = ∠CEM = 1/2∠AEC = 33°. 在△AEC中，
∵EA = EC，∠AEH = ∠CEH，
∴EH⊥AC，AH = CH.
∵直线l是对称轴，
∴MQ = QN，AB⊥l，CD⊥l，MN⊥l.
∴AB//CD//MN.
∴AC⊥AB.
∴AC的长为这张圆凳的高.
∵这张圆凳的高为42.9 cm，
∴AC = 42.9 cm.
∴AH = CH = 429/20 cm. 在Rt△AEH中，
∵sin∠AEH = AH/AE，
∴设AE = x cm，则11/20≈429/20/x，解得x = 39. 经检验，x = 39是原分式方程的解，且符合题意.
∴AE = 39 cm.
∵tan∠AEH = AH/HE，
∴设EH = y cm，则13/20≈429/20/y，解得y = 33. 经检验，y = 33是原分式方程的解，且符合题意.
∴EH = 33 cm.
∵ME = AE = 39 cm，
∴MH = 6 cm.
∵该图形为轴对称图形，且易得HQ = 1/2AB，
∴MQ = MH + HQ = MH + 1/2AB = 6 + 15 = 21(cm).
∴MN = 42 cm