《2025年通城学典非常课课通九年级数学下册苏科版江苏专版》

10. 已知锐角$\alpha$满足$2\cos\alpha(\cos\alpha + 1)=5\cos\alpha - 1$，求锐角$\alpha$的度数.

答案： 原方程可变为$2\cos^{2}\alpha - 3\cos\alpha + 1 = 0$. $\therefore$ $(2\cos\alpha - 1)(\cos\alpha - 1)=0$，解得$\cos\alpha=\frac{1}{2}$或$\cos\alpha = 1$. $\because$ $\alpha$为锐角，$\therefore$ $0＜\cos\alpha＜1$. $\therefore$ $\cos\alpha=\frac{1}{2}$. $\therefore$ 锐角$\alpha$的度数为$60^{\circ}$

11.（2024·雅安改编）如图，$AB$是$\odot O$的直径，$C$是$\odot O$上的一点，$P$是$BA$延长线上的一点，连接$AC、BC、PC$，$\angle PCA = \angle B$，$CD\perp AB$于点$D$.
（1）求证：$PC$是$\odot O$的切线；
（2）若$\sin B = \frac{1}{2}$，求证：$AC = AP$；
（3）若$PA = 4$，$BD = 6$，求$\angle BAC$的度数.

答案：
(1) 连接$OC$. $\because$ $AB$是$\odot O$的直径，$\therefore$ $\angle ACB = 90^{\circ}$. $\therefore$ $\angle BCO+\angle OCA = 90^{\circ}$. $\because$ $OB = OC$，$\therefore$ $\angle B=\angle BCO$. $\because$ $\angle PCA=\angle B$，$\therefore$ $\angle PCA=\angle BCO$. $\therefore$ $\angle PCA+\angle OCA = 90^{\circ}$. $\therefore$ $OC\perp PC$. $\because$ 点$C$在$\odot O$上，$\therefore$ $PC$是$\odot O$的切线
(2) $\because$ $\sin B=\frac{1}{2}$，$\angle ACB = 90^{\circ}$，$\therefore$ $\angle B = 30^{\circ}$. $\therefore$ $\angle PCA=\angle B = 30^{\circ}$，$\angle CAB = 90^{\circ}-30^{\circ}=60^{\circ}$. $\because$ $\angle CAB=\angle P+\angle PCA$，$\therefore$ $\angle P=\angle CAB-\angle PCA = 30^{\circ}$. $\therefore$ $\angle PCA=\angle P = 30^{\circ}$. $\therefore$ $AC = AP$
(3) 设$AD = x$. 由题意，得$\angle BCD+\angle B = 90^{\circ}$，$\angle BCD+\angle DCA = 90^{\circ}$，$\therefore$ $\angle B=\angle DCA$. $\because$ $\angle BDC=\angle CDA = 90^{\circ}$，$\therefore$ $\triangle BCD\sim\triangle CAD$. $\therefore$ $\frac{BD}{CD}=\frac{CD}{AD}$. $\therefore$ $CD^{2}=AD\cdot BD = 6x$. $\because$ $\angle P=\angle P$，$\angle PCA=\angle B$，$\therefore$ $\triangle PAC\sim\triangle PCB$. $\therefore$ $\frac{PA}{PC}=\frac{PC}{PB}$. $\therefore$ $PC^{2}=PA\cdot PB = 4(6 + 4 + x)=4(10 + x)$. 在$Rt\triangle PCD$中，$\because$ $\angle CDP = 90^{\circ}$，$\therefore$ $PD^{2}+CD^{2}=PC^{2}$，即$(4 + x)^{2}+6x = 4(10 + x)$. 整理，得$x^{2}+10x - 24 = 0$，解得$x_{1}=2$，$x_{2}=-12$（不合题意，舍去）. $\therefore$ $AD = 2$，$CD^{2}=6\times2 = 12$. $\therefore$ $CD = 2\sqrt{3}$. $\because$ $\angle ADC = 90^{\circ}$，$\therefore$ $\tan\angle DAC=\frac{CD}{AD}=\frac{2\sqrt{3}}{2}=\sqrt{3}$. $\therefore$ 锐角$\angle BAC$的度数为$60^{\circ}$

12.（2023·菏泽改编）如图，抛物线$y = -x^{2}+bx + c$与$x$轴交于$A、B$两点，与$y$轴交于点$C(0,4)$，其对称轴为直线$x = -\frac{3}{2}$，$D$是线段$OC$上的一动点，连接$AD、BD$. 将$\triangle ABD$沿直线$AD$翻折，得到$\triangle AB'D$，当点$B'$恰好落在抛物线的对称轴上时，$\cos\angle B'AB$的值为（ ）

A. $\frac{\sqrt{3}}{3}$
B. $\frac{1}{2}$
C. $\frac{\sqrt{2}}{2}$
D. $\frac{\sqrt{3}}{2}$

答案：
B 解析：如图，设直线$x = -\frac{3}{2}$与$x$轴交于点$H$. $\because$ 抛物线$y=-x^{2}+bx + c$与$y$轴交于点$C(0,4)$，$\therefore$ 易得$c = 4$. $\because$ 对称轴为直线$x = -\frac{3}{2}$，$\therefore$ $-\frac{b}{-2}=-\frac{3}{2}$，解得$b=-3$. $\therefore$ 抛物线对应的函数表达式为$y=-x^{2}-3x + 4$. 令$-x^{2}-3x + 4 = 0$，解得$x_{1}=1$，$x_{2}=-4$. $\therefore$ 点$A$的坐标为$(-4,0)$，点$B$的坐标为$(1,0)$. $\therefore$ $OA = 4$，$AB = 1-(-4)=5$. 由翻折，可得$AB' = AB = 5$. $\because$ 对称轴为直线$x = -\frac{3}{2}$，$\therefore$ $AH = -\frac{3}{2}-(-4)=\frac{5}{2}$. $\because$ $AB' = AB = 5 = 2AH$. $\therefore$ $\sin\angle AB'H=\frac{AH}{AB'}=\frac{1}{2}$. $\therefore$ 锐角$\angle AB'H$的度数为$30^{\circ}$. $\therefore$ $\angle B'AB = 90^{\circ}-30^{\circ}=60^{\circ}$. $\therefore$ $\cos\angle B'AB=\frac{1}{2}$.

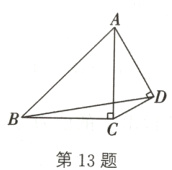
13.（宝应一模）将两个直角三角形拼成如图所示的四边形$ABCD$，一边重合，若$\angle CAB = 45^{\circ}$，$\angle CAD = 30^{\circ}$，连接$BD$，则$\tan\angle DBC =$_______.

答案：
$\frac{4-\sqrt{3}}{13}$ 解析：由题意，易得$\angle ACD = 60^{\circ}$. 如图，过点$D$作$DH\perp BC$，交$BC$的延长线于点$H$，则$\angle DCH = 180^{\circ}-\angle ACB-\angle ACD = 180^{\circ}-90^{\circ}-60^{\circ}=30^{\circ}$. 在$Rt\triangle CDH$中，设$DH = x$，则$\sin30^{\circ}=\frac{DH}{CD}=\frac{1}{2}$，$\tan30^{\circ}=\frac{DH}{CH}=\frac{\sqrt{3}}{3}$. $\therefore$ $CD = 2x$，$CH = \sqrt{3}x$. 在$Rt\triangle ACD$中，$\because$ $\angle ADC = 90^{\circ}$，$\angle CAD = 30^{\circ}$，$\therefore$ $\sin30^{\circ}=\frac{CD}{AC}=\frac{1}{2}$，即$AC = 4x$. $\therefore$ 易得$BC = AC = 4x$. $\therefore$ $BH = BC + CH = 4x+\sqrt{3}x=(4+\sqrt{3})x$. 在$Rt\triangle BDH$中，$\because$ $\angle DHB = 90^{\circ}$，$\therefore$ $\tan\angle DBC=\frac{DH}{BH}=\frac{x}{(4+\sqrt{3})x}=\frac{4-\sqrt{3}}{13}$.

14. 如图，$Rt\triangle ABC\cong Rt\triangle DEC$，$\angle ACB = \angle DCE = 90^{\circ}$，$\angle E = 30^{\circ}$，$D$为$AB$的中点，$AC = 1$.将$\triangle DEC$绕点$D$按顺时针方向旋转至$\triangle DE'C'$处，使$E'D、C'D$分别与$Rt\triangle ABC$的直角边$BC$交于点$M、N$，则当$\triangle DMN$为等边三角形时，求$AM$的长.

答案： $\because$ $\angle E = 30^{\circ}$，$\angle DCE = 90^{\circ}$，$\therefore$ $\angle CDE = 60^{\circ}$. $\because$ $Rt\triangle ABC\cong Rt\triangle DEC$，$\therefore$ $\angle CAB=\angle CDE = 60^{\circ}$，$AC = DC$. $\therefore$ $\triangle ACD$是等边三角形. $\therefore$ $AD = AC = 1$，$\angle ACD = 60^{\circ}$. 又$\because$ $\angle ECA+\angle ACD=\angle DCE = 90^{\circ}$，$\therefore$ $\angle ECA = 30^{\circ}$. 同理，$\angle DCM = 30^{\circ}$. $\because$ $\triangle DMN$是等边三角形，$\therefore$ $\angle DMN = 60^{\circ}$. $\therefore$ $\angle CDM=\angle DMN-\angle DCM = 30^{\circ}$. $\therefore$ $\angle CDM=\angle DCM$. $\therefore$ $MD = MC$，$\angle ADM=\angle ADC+\angle CDM = 90^{\circ}$. $\because$ $AC = AD$，$\angle ACM=\angle ADM = 90^{\circ}$，$MC = MD$，$\therefore$ $\triangle ACM\cong\triangle ADM$. $\therefore$ $\angle CAM=\angle DAM=\frac{1}{2}\angle CAB = 30^{\circ}$. $\therefore$ 在$Rt\triangle ADM$中，$\cos\angle DAM=\frac{AD}{AM}=\frac{\sqrt{3}}{2}$，即$AM=\frac{2\sqrt{3}}{3}$