2025年通城学典非常课课通九年级数学下册苏科版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典非常课课通九年级数学下册苏科版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
9. 如图,在四边形ABCD中,∠ACB = ∠CAD = 90°,点E在BC上,AE//DC,EF⊥AB,垂足为F.
(1)求证:四边形AECD是平行四边形;
(2)若AE平分∠BAC,BE = 5,AD = 3,求cos B的值.

(1)求证:四边形AECD是平行四边形;
(2)若AE平分∠BAC,BE = 5,AD = 3,求cos B的值.

答案:
(1) $\because \angle ACB=\angle CAD = 90^{\circ}$,$\therefore AD// CE$.$\because AE// DC$,$\therefore$ 四边形$AECD$是平行四边形
(2) $\because$ 四边形$AECD$是平行四边形,$\therefore EC = AD = 3$. 又$\because AE$平分$\angle BAC$,$EF\perp AB$,$\angle ACB = 90^{\circ}$,$\therefore EF = EC = 3$.$\because EF\perp AB$,$\therefore \angle BFE = 90^{\circ}$. 在$Rt\triangle BFE$中,由勾股定理,得$BF=\sqrt{BE^{2}-EF^{2}}=\sqrt{5^{2}-3^{2}} = 4$.$\therefore \cos B=\frac{BF}{BE}=\frac{4}{5}$
(1) $\because \angle ACB=\angle CAD = 90^{\circ}$,$\therefore AD// CE$.$\because AE// DC$,$\therefore$ 四边形$AECD$是平行四边形
(2) $\because$ 四边形$AECD$是平行四边形,$\therefore EC = AD = 3$. 又$\because AE$平分$\angle BAC$,$EF\perp AB$,$\angle ACB = 90^{\circ}$,$\therefore EF = EC = 3$.$\because EF\perp AB$,$\therefore \angle BFE = 90^{\circ}$. 在$Rt\triangle BFE$中,由勾股定理,得$BF=\sqrt{BE^{2}-EF^{2}}=\sqrt{5^{2}-3^{2}} = 4$.$\therefore \cos B=\frac{BF}{BE}=\frac{4}{5}$
10.(2023·扬州)如图,在△ABC中,∠ACB = 90°,D是AB上一点,且∠BCD = $\frac{1}{2}$∠A,点O在BC上,以点O为圆心的圆经过C、D两点.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若sin B = $\frac{3}{5}$,⊙O的半径为3,求AC的长.

(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若sin B = $\frac{3}{5}$,⊙O的半径为3,求AC的长.

答案:
(1) 直线$AB$与$\odot O$相切 理由:连接$OD$. 由“圆周角的度数等于它所对弧上的圆心角度数的一半”,可知$\angle BCD=\frac{1}{2}\angle BOD$.$\because \angle BCD=\frac{1}{2}\angle A$,$\therefore \angle BOD=\angle A$.$\because \angle ACB = 90^{\circ}$,$\therefore \angle A+\angle B = 90^{\circ}$.$\therefore \angle BOD+\angle B = 90^{\circ}$.$\therefore \angle BDO = 90^{\circ}$.$\therefore OD\perp AB$.$\because$ 直线$AB$上的点$D$在$\odot O$上,$\therefore$ 直线$AB$与$\odot O$相切.
(2) 在$Rt\triangle BOD$中,$\because \angle BDO = 90^{\circ}$,$\sin B=\frac{OD}{OB}$.$\because \odot O$的半径为$3$,$\therefore OD = OC = 3$.$\therefore \frac{3}{OB}=\frac{3}{5}$,解得$OB = 5$.$\therefore BC = OB + OC = 8$. 在$Rt\triangle ACB$中,$\because \angle ACB = 90^{\circ}$,$\sin B=\frac{AC}{AB}=\frac{3}{5}$. 设$AC = 3k$,则$AB = 5k$.$\therefore BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{(5k)^{2}-(3k)^{2}} = 4k$.$\therefore 4k = 8$,解得$k = 2$.$\therefore AC = 3k = 3\times2 = 6$
(1) 直线$AB$与$\odot O$相切 理由:连接$OD$. 由“圆周角的度数等于它所对弧上的圆心角度数的一半”,可知$\angle BCD=\frac{1}{2}\angle BOD$.$\because \angle BCD=\frac{1}{2}\angle A$,$\therefore \angle BOD=\angle A$.$\because \angle ACB = 90^{\circ}$,$\therefore \angle A+\angle B = 90^{\circ}$.$\therefore \angle BOD+\angle B = 90^{\circ}$.$\therefore \angle BDO = 90^{\circ}$.$\therefore OD\perp AB$.$\because$ 直线$AB$上的点$D$在$\odot O$上,$\therefore$ 直线$AB$与$\odot O$相切.
(2) 在$Rt\triangle BOD$中,$\because \angle BDO = 90^{\circ}$,$\sin B=\frac{OD}{OB}$.$\because \odot O$的半径为$3$,$\therefore OD = OC = 3$.$\therefore \frac{3}{OB}=\frac{3}{5}$,解得$OB = 5$.$\therefore BC = OB + OC = 8$. 在$Rt\triangle ACB$中,$\because \angle ACB = 90^{\circ}$,$\sin B=\frac{AC}{AB}=\frac{3}{5}$. 设$AC = 3k$,则$AB = 5k$.$\therefore BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{(5k)^{2}-(3k)^{2}} = 4k$.$\therefore 4k = 8$,解得$k = 2$.$\therefore AC = 3k = 3\times2 = 6$
11. 如图,在菱形纸片ABCD中,AB = 2,∠A = 60°,将菱形纸片翻折,使点A落在边CD的中点E处,折痕为FG,点F、G分别在边AB、AD上,则cos∠EFG的值为( )

A. $\frac{\sqrt{21}}{7}$
B. $\frac{\sqrt{15}}{5}$
C. $\frac{2\sqrt{3}}{15}$
D. $\frac{3\sqrt{3}}{35}$

A. $\frac{\sqrt{21}}{7}$
B. $\frac{\sqrt{15}}{5}$
C. $\frac{2\sqrt{3}}{15}$
D. $\frac{3\sqrt{3}}{35}$
答案:
A 解析:如图,连接$BE$、$BD$,连接$AE$,交$FG$于点$O$.$\because$ 四边形$ABCD$为菱形,$\therefore AD = BC = CD = AB = 2$.$\therefore \triangle BDC$为等腰三角形. 由题意,得$\angle C=\angle BAD = 60^{\circ}$,$\therefore \triangle BDC$为等边三角形.$\therefore BD = BC = CD$.$\because E$是$CD$的中点,$\therefore BE\perp CD$,$CE = DE=\frac{1}{2}CD = 1$. 在$Rt\triangle BCE$中,由勾股定理,得$BE=\sqrt{BC^{2}-CE^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$. 由题意,得$AB// CD$,$BE\perp CD$,$\therefore BE\perp AB$. 在$Rt\triangle ABE$中,由勾股定理,得$AE=\sqrt{AB^{2}+BE^{2}}=\sqrt{2^{2}+(\sqrt{3})^{2}}=\sqrt{7}$. 设$EF = x$. 由折叠的性质,可知$EF = AF$,$FG$垂直平分$AE$.$\therefore BF = 2 - x$,$OE=\frac{1}{2}AE=\frac{\sqrt{7}}{2}$. 在$Rt\triangle BEF$中,由勾股定理,得$BF^{2}+BE^{2}=EF^{2}$,$\therefore (2 - x)^{2}+(\sqrt{3})^{2}=x^{2}$,解得$x=\frac{7}{4}$,即$EF=\frac{7}{4}$. 在$Rt\triangle EOF$中,由勾股定理,得$OF=\sqrt{EF^{2}-OE^{2}}=\sqrt{(\frac{7}{4})^{2}-(\frac{\sqrt{7}}{2})^{2}}=\frac{\sqrt{21}}{4}$.$\therefore \cos\angle EFG=\frac{OF}{EF}=\frac{\frac{\sqrt{21}}{4}}{\frac{7}{4}}=\frac{\sqrt{21}}{7}$.

A 解析:如图,连接$BE$、$BD$,连接$AE$,交$FG$于点$O$.$\because$ 四边形$ABCD$为菱形,$\therefore AD = BC = CD = AB = 2$.$\therefore \triangle BDC$为等腰三角形. 由题意,得$\angle C=\angle BAD = 60^{\circ}$,$\therefore \triangle BDC$为等边三角形.$\therefore BD = BC = CD$.$\because E$是$CD$的中点,$\therefore BE\perp CD$,$CE = DE=\frac{1}{2}CD = 1$. 在$Rt\triangle BCE$中,由勾股定理,得$BE=\sqrt{BC^{2}-CE^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$. 由题意,得$AB// CD$,$BE\perp CD$,$\therefore BE\perp AB$. 在$Rt\triangle ABE$中,由勾股定理,得$AE=\sqrt{AB^{2}+BE^{2}}=\sqrt{2^{2}+(\sqrt{3})^{2}}=\sqrt{7}$. 设$EF = x$. 由折叠的性质,可知$EF = AF$,$FG$垂直平分$AE$.$\therefore BF = 2 - x$,$OE=\frac{1}{2}AE=\frac{\sqrt{7}}{2}$. 在$Rt\triangle BEF$中,由勾股定理,得$BF^{2}+BE^{2}=EF^{2}$,$\therefore (2 - x)^{2}+(\sqrt{3})^{2}=x^{2}$,解得$x=\frac{7}{4}$,即$EF=\frac{7}{4}$. 在$Rt\triangle EOF$中,由勾股定理,得$OF=\sqrt{EF^{2}-OE^{2}}=\sqrt{(\frac{7}{4})^{2}-(\frac{\sqrt{7}}{2})^{2}}=\frac{\sqrt{21}}{4}$.$\therefore \cos\angle EFG=\frac{OF}{EF}=\frac{\frac{\sqrt{21}}{4}}{\frac{7}{4}}=\frac{\sqrt{21}}{7}$.

12.(乐山期末)如图,点A的坐标为(4,3),B为直线y = -2上的一个动点,点C的坐标为(0,n),-2 < n < 3,AC⊥BC于点C,连接AB. 若直线AB与x轴的正半轴所夹的锐角为α,则当sin α的值最大时,n的值为______.


答案:
$\frac{1}{2}$ 解析:如图,设直线$y = - 2$交$y$轴于点$G$,分别过点$A$作$AM\perp y$轴于点$M$、$AN\perp BG$于点$N$,则$CM = 3 - n$,$AM = 4$,$CG = n - (-2)=n + 2$,$AN = 3 - (-2)=5$.$\because BN// x$轴,$\therefore \angle ABN=\alpha$. 在$Rt\triangle ABN$中,$\because \angle ANB = 90^{\circ}$,$\therefore \tan\alpha=\frac{AN}{BN}=\frac{5}{BN}$.$\because$ 当$\sin\alpha$的值最大时,$\tan\alpha$也取最大值,$\therefore BN$的长取最小值,此时$BG$长的值最大. $\because \angle MAC = 90^{\circ}-\angle ACM=\angle GCB$,$\angle AMC=\angle CGB = 90^{\circ}$,$\therefore \triangle ACM\sim\triangle CBG$.$\therefore \frac{CM}{BG}=\frac{AM}{CG}$,即$\frac{3 - n}{BG}=\frac{4}{n + 2}$.$\therefore BG=-\frac{1}{4}(n - 3)(n + 2)=-\frac{1}{4}(n-\frac{1}{2})^{2}+\frac{25}{16}$.$\because -\frac{1}{4}<0$,$-2 < n < 3$,$\therefore$ 当$n=\frac{1}{2}$时,$BG$的长取最大值,此时$BN$的长取最小值,$\sin\alpha$取最大值. $\therefore n=\frac{1}{2}$.

$\frac{1}{2}$ 解析:如图,设直线$y = - 2$交$y$轴于点$G$,分别过点$A$作$AM\perp y$轴于点$M$、$AN\perp BG$于点$N$,则$CM = 3 - n$,$AM = 4$,$CG = n - (-2)=n + 2$,$AN = 3 - (-2)=5$.$\because BN// x$轴,$\therefore \angle ABN=\alpha$. 在$Rt\triangle ABN$中,$\because \angle ANB = 90^{\circ}$,$\therefore \tan\alpha=\frac{AN}{BN}=\frac{5}{BN}$.$\because$ 当$\sin\alpha$的值最大时,$\tan\alpha$也取最大值,$\therefore BN$的长取最小值,此时$BG$长的值最大. $\because \angle MAC = 90^{\circ}-\angle ACM=\angle GCB$,$\angle AMC=\angle CGB = 90^{\circ}$,$\therefore \triangle ACM\sim\triangle CBG$.$\therefore \frac{CM}{BG}=\frac{AM}{CG}$,即$\frac{3 - n}{BG}=\frac{4}{n + 2}$.$\therefore BG=-\frac{1}{4}(n - 3)(n + 2)=-\frac{1}{4}(n-\frac{1}{2})^{2}+\frac{25}{16}$.$\because -\frac{1}{4}<0$,$-2 < n < 3$,$\therefore$ 当$n=\frac{1}{2}$时,$BG$的长取最大值,此时$BN$的长取最小值,$\sin\alpha$取最大值. $\therefore n=\frac{1}{2}$.

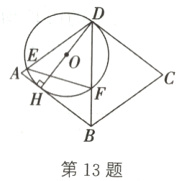
13.(2023·荆州)如图,在菱形ABCD中,DH⊥AB于点H,以DH为直径的⊙O分别交AD、BD于点E、F,连接EF.
(1)求证:
①CD是⊙O的切线;
②△DEF∽△DBA.
(2)若AB = 5,BD = 6,求sin∠DFE的值.
(1)求证:
①CD是⊙O的切线;
②△DEF∽△DBA.
(2)若AB = 5,BD = 6,求sin∠DFE的值.

答案:
(1) ① $\because$ 四边形$ABCD$是菱形,$\therefore AB// CD$.$\because DH\perp AB$,$\therefore \angle CDH=\angle DHA = 90^{\circ}$.$\therefore CD\perp OD$. 又$\because OD$为$\odot O$的半径,$\therefore CD$是$\odot O$的切线 ② 如图,连接$HF$.$\because \overset{\frown}{DF}=\overset{\frown}{CF}$,$\therefore \angle DEF=\angle DHF$.$\because DH$为$\odot O$的直径,$\therefore \angle DFH = 90^{\circ}$.$\because \angle DHB = 90^{\circ}$,$\therefore$ 易得$\angle DHF=\angle DEF=\angle DBA$. 又$\because \angle EDF=\angle BDA$,$\therefore \triangle DEF\sim\triangle DBA$
(2) 如图,连接$AC$,交$BD$于点$G$. 在菱形$ABCD$中,$AC\perp BD$,$AB = AD$,$AG = GC$,$DG = GB=\frac{1}{2}BD = 3$.$\therefore$ 在$Rt\triangle AGB$中,$AG=\sqrt{AB^{2}-GB^{2}} = 4$.$\therefore AC = 2AG = 8$.$\because S_{菱形ABCD}=\frac{1}{2}AC\cdot BD = AB\cdot DH$,$\therefore DH=\frac{24}{5}$. 在$Rt\triangle ADH$中,$\sin\angle DAH=\frac{DH}{AD}=\frac{DH}{AB}=\frac{\frac{24}{5}}{5}=\frac{24}{25}$.$\because \triangle DEF\sim\triangle DBA$,$\therefore \angle DFE=\angle DAH$.$\therefore \sin\angle DFE=\sin\angle DAH=\frac{24}{25}$

(1) ① $\because$ 四边形$ABCD$是菱形,$\therefore AB// CD$.$\because DH\perp AB$,$\therefore \angle CDH=\angle DHA = 90^{\circ}$.$\therefore CD\perp OD$. 又$\because OD$为$\odot O$的半径,$\therefore CD$是$\odot O$的切线 ② 如图,连接$HF$.$\because \overset{\frown}{DF}=\overset{\frown}{CF}$,$\therefore \angle DEF=\angle DHF$.$\because DH$为$\odot O$的直径,$\therefore \angle DFH = 90^{\circ}$.$\because \angle DHB = 90^{\circ}$,$\therefore$ 易得$\angle DHF=\angle DEF=\angle DBA$. 又$\because \angle EDF=\angle BDA$,$\therefore \triangle DEF\sim\triangle DBA$
(2) 如图,连接$AC$,交$BD$于点$G$. 在菱形$ABCD$中,$AC\perp BD$,$AB = AD$,$AG = GC$,$DG = GB=\frac{1}{2}BD = 3$.$\therefore$ 在$Rt\triangle AGB$中,$AG=\sqrt{AB^{2}-GB^{2}} = 4$.$\therefore AC = 2AG = 8$.$\because S_{菱形ABCD}=\frac{1}{2}AC\cdot BD = AB\cdot DH$,$\therefore DH=\frac{24}{5}$. 在$Rt\triangle ADH$中,$\sin\angle DAH=\frac{DH}{AD}=\frac{DH}{AB}=\frac{\frac{24}{5}}{5}=\frac{24}{25}$.$\because \triangle DEF\sim\triangle DBA$,$\therefore \angle DFE=\angle DAH$.$\therefore \sin\angle DFE=\sin\angle DAH=\frac{24}{25}$

查看更多完整答案,请扫码查看


