2025年通城学典非常课课通九年级数学下册苏科版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典非常课课通九年级数学下册苏科版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1.(2024·沭阳期末)如图,在Rt△ACB中,∠C = 90°,AC = 3BC,则sin A的值为( )

A. $\frac{1}{3}$
B. $\frac{\sqrt{2}}{4}$
C. $\frac{\sqrt{10}}{10}$
D. $\frac{3\sqrt{10}}{10}$

A. $\frac{1}{3}$
B. $\frac{\sqrt{2}}{4}$
C. $\frac{\sqrt{10}}{10}$
D. $\frac{3\sqrt{10}}{10}$
答案:
C
2.(邵东期末)在△ABC中,∠C = 90°,若tan A = $\frac{3}{4}$,则cos A的值为( )
A. $\frac{3}{5}$
B. $\frac{4}{5}$
C. $\frac{3}{4}$
D. $\frac{4}{3}$
A. $\frac{3}{5}$
B. $\frac{4}{5}$
C. $\frac{3}{4}$
D. $\frac{4}{3}$
答案:
B
3.(2024·临夏)如图,在△ABC中,AB = AC = 5,sin B = $\frac{4}{5}$,则BC的长是( )
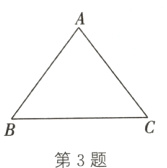
A. 3
B. 6
C. 8
D. 9

A. 3
B. 6
C. 8
D. 9
答案:
B
4.(2023·陕西)如图,在6×7的网格中,每个小正方形的边长均为1.若点A、B、C都在格点上,则sin B的值为( )

A. $\frac{2\sqrt{13}}{13}$
B. $\frac{3\sqrt{13}}{13}$
C. $\frac{2}{3}$
D. $\frac{\sqrt{5}}{4}$

A. $\frac{2\sqrt{13}}{13}$
B. $\frac{3\sqrt{13}}{13}$
C. $\frac{2}{3}$
D. $\frac{\sqrt{5}}{4}$
答案:
A
5.(2024·历城期末改编)有6个大小相同的小正方形,按如图所示的方式恰好放置在△ABC中,则sin B的值为______.


答案:
$\frac{\sqrt{5}}{5}$
6. 如图,在平面直角坐标系中,点A的坐标为(3,3),点B的坐标为(7,0),则sin∠ABO的值为______.
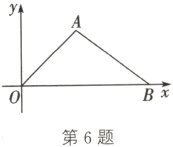

答案:
$\frac{3}{5}$
7.(建平一模)如图,在Rt△ABC中,∠ACB = 90°,CE是斜边AB上的中线,过点E作EF⊥AB,交AC于点F. 若BC = 4,△AEF的面积为5,则sin∠CEF的值为______.


答案:
$\frac{3}{5}$
8.(2024·浙江)如图,在△ABC中,AD⊥BC,AE是边BC上的中线,AB = 10,AD = 6,tan∠ACB = 1. 求:
(1)BC的长;
(2)sin∠DAE的值.
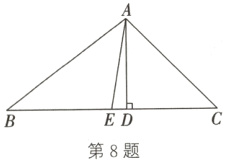
(1)BC的长;
(2)sin∠DAE的值.

答案:
(1) $\because AD\perp BC$,$\therefore \angle ADB=\angle ADC = 90^{\circ}$.$\therefore BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{10^{2}-6^{2}} = 8$.$\because \angle ADC = 90^{\circ}$,$\tan\angle ACB = 1$,即$\tan\angle ACD = 1$,$\therefore \frac{AD}{CD}=1$.$\therefore CD = AD = 6$.$\therefore BC = BD + CD = 8 + 6 = 14$
(2) $\because AE$是边$BC$上的中线,$\therefore CE=\frac{1}{2}BC=\frac{1}{2}\times14 = 7$.$\therefore DE = CE - CD = 7 - 6 = 1$.$\because \angle ADB = 90^{\circ}$,即$\angle ADE = 90^{\circ}$,$\therefore AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{6^{2}+1^{2}}=\sqrt{37}$.$\therefore \sin\angle DAE=\frac{DE}{AE}=\frac{1}{\sqrt{37}}=\frac{\sqrt{37}}{37}$
(1) $\because AD\perp BC$,$\therefore \angle ADB=\angle ADC = 90^{\circ}$.$\therefore BD=\sqrt{AB^{2}-AD^{2}}=\sqrt{10^{2}-6^{2}} = 8$.$\because \angle ADC = 90^{\circ}$,$\tan\angle ACB = 1$,即$\tan\angle ACD = 1$,$\therefore \frac{AD}{CD}=1$.$\therefore CD = AD = 6$.$\therefore BC = BD + CD = 8 + 6 = 14$
(2) $\because AE$是边$BC$上的中线,$\therefore CE=\frac{1}{2}BC=\frac{1}{2}\times14 = 7$.$\therefore DE = CE - CD = 7 - 6 = 1$.$\because \angle ADB = 90^{\circ}$,即$\angle ADE = 90^{\circ}$,$\therefore AE=\sqrt{AD^{2}+DE^{2}}=\sqrt{6^{2}+1^{2}}=\sqrt{37}$.$\therefore \sin\angle DAE=\frac{DE}{AE}=\frac{1}{\sqrt{37}}=\frac{\sqrt{37}}{37}$
查看更多完整答案,请扫码查看


