2025年通城学典非常课课通九年级数学下册苏科版江苏专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年通城学典非常课课通九年级数学下册苏科版江苏专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
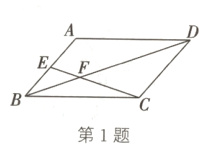
1.(2024·沭阳期末)如图,在□ABCD中,E是AB的中点,EC交BD于点F,那么EF与CF的长度比是( )
A. 2∶1
B. 1∶3
C. 1∶2
D. 3∶1

A. 2∶1
B. 1∶3
C. 1∶2
D. 3∶1
答案:
C
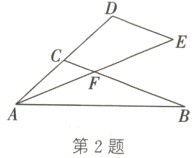
2.(2024·重庆A卷改编)如图,在△ABC中,延长AC至点D,使CD = CA,过点D作DE//CB,且DE = DC,连接AE,交BC于点F. 若∠CAB = ∠CFA,CF = 1,则BF的长为( )
A. 2
B. 2.5
C. 3
D. 3.5

A. 2
B. 2.5
C. 3
D. 3.5
答案:
C
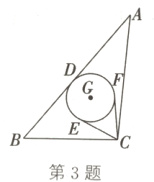
3.(2023·无锡期末)如图,在△ABC中,∠A = 35°,∠B = 50°,点G是△ABC的重心,AB的中点为D,以点G为圆心、GD长为半径画⊙G,过点C作⊙G的两条切线CE、CF,其中E、F为切点,则∠BCE + ∠ACF的大小为( )
A. 30°
B. 35°
C. 40°
D. 45°

A. 30°
B. 35°
C. 40°
D. 45°
答案:
B
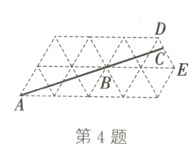
4.(2024·丹阳期中)如图所示为由一些边长为1的等边三角形组成的网格,其中A、B、D、E均是等边三角形的顶点,延长AB,交DE于点C,则$\frac{DC}{CE}$的值为( )
A. $\frac{\sqrt{3}}{3}$
B. $\frac{\sqrt{3}}{2}$
C. $\frac{\sqrt{2}}{2}$
D. $\frac{1}{2}$

A. $\frac{\sqrt{3}}{3}$
B. $\frac{\sqrt{3}}{2}$
C. $\frac{\sqrt{2}}{2}$
D. $\frac{1}{2}$
答案:
D
5.(2024·连云港期中改编)如图,一次函数y = $\frac{1}{2}$x + b的图像分别与x轴、y轴交于点A、B,与函数y = $\frac{k}{x}$(x>0)的图像交于点C,连接OC. 若点A的坐标为(-4,0),AB = 2BC,则△AOC的面积为______.
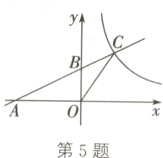

答案:
6
6.(2024·锡山期中改编)如图,△ABC和△CDE都是等边三角形,点G在CA的延长线上. GB = GE. 若BE + CG = 20,$\frac{AG}{BE}=\frac{3}{2}$,则AF的长为______.
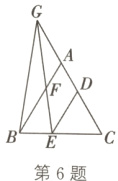

答案:
$\frac{18}{5}$
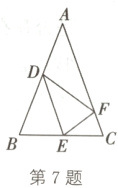
7.(2023·路北期末)如图,在△ABC中,AB = AC,点E在边BC上移动(不与点B、C重合),∠DEF = ∠B,且点D、F分别在边AB、AC上.
(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点时,求证:FE平分∠DFC.
(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点时,求证:FE平分∠DFC.

答案:
(1) $\because AB = AC$,$\therefore \angle B=\angle C$.$\because \angle DEF+\angle CEF=\angle B+\angle BDE$,$\angle DEF = \angle B$,$\therefore \angle CEF = \angle BDE$.$\therefore \triangle BDE\backsim\triangle CEF$
(2) $\because \triangle BDE\backsim\triangle CEF$,$\therefore \frac{BE}{CF}=\frac{DE}{EF}$.$\because E$是$BC$的中点,$\therefore BE = CE$.$\therefore \frac{CE}{CF}=\frac{DE}{EF}$,即$\frac{CE}{ED}=\frac{CF}{EF}$.$\because \angle B=\angle C$,$\angle DEF=\angle B$,$\therefore \angle C=\angle DEF$.$\therefore \triangle CEF\backsim\triangle EDF$.$\therefore \angle CFE=\angle EFD$.$\therefore FE$平分$\angle DFC$.
(1) $\because AB = AC$,$\therefore \angle B=\angle C$.$\because \angle DEF+\angle CEF=\angle B+\angle BDE$,$\angle DEF = \angle B$,$\therefore \angle CEF = \angle BDE$.$\therefore \triangle BDE\backsim\triangle CEF$
(2) $\because \triangle BDE\backsim\triangle CEF$,$\therefore \frac{BE}{CF}=\frac{DE}{EF}$.$\because E$是$BC$的中点,$\therefore BE = CE$.$\therefore \frac{CE}{CF}=\frac{DE}{EF}$,即$\frac{CE}{ED}=\frac{CF}{EF}$.$\because \angle B=\angle C$,$\angle DEF=\angle B$,$\therefore \angle C=\angle DEF$.$\therefore \triangle CEF\backsim\triangle EDF$.$\therefore \angle CFE=\angle EFD$.$\therefore FE$平分$\angle DFC$.
8.(2024·肇源期中改编)如图,在△ABC中,AC = 16 cm,BC = 8 cm,点P从点A开始沿AC向点C以4 cm/s的速度运动,点Q从点C开始沿CB向点B以2 cm/s的速度运动. 如果点P、Q同时运动,那么何时△QCP与△ABC相似?
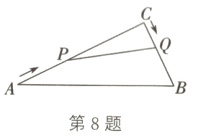

答案:
设经过$t\ s$,$\triangle QCP$与$\triangle ABC$相似,则$AP = 4t\ cm$,$PC=(16 - 4t)cm$,$CQ = 2t\ cm$. ① 当$\triangle PCQ\backsim\triangle ACB$时,$\frac{PC}{AC}=\frac{CQ}{CB}$,即$\frac{16 - 4t}{16}=\frac{2t}{8}$,解得$t = 2$. ② 当$\triangle PCQ\backsim\triangle BCA$时,$\frac{PC}{BC}=\frac{CQ}{CA}$,即$\frac{16 - 4t}{8}=\frac{2t}{16}$,解得$t=\frac{16}{5}$. 所以经过$2\ s$或$\frac{16}{5}\ s$,$\triangle QCP$与$\triangle ABC$相似.
查看更多完整答案,请扫码查看


