2025年千里马单元测试卷八年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年千里马单元测试卷八年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第111页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
14. 为了满足不同顾客对保温杯保温时效的要求,保温杯生产厂家研发了甲、乙两款保温杯. 现从甲、乙两款中各随机抽取了5个保温杯,测得保温时效(单位:h)如下表:
|甲|11|12|13|14|15|
|----|----|----|----|----|----|
|乙|x|6|7|5|8|
如果甲、乙两款保温杯保温时效的方差是相等的,那么x =________.
|甲|11|12|13|14|15|
|----|----|----|----|----|----|
|乙|x|6|7|5|8|
如果甲、乙两款保温杯保温时效的方差是相等的,那么x =________.
答案:
4或9
15. 已知在一个样本中,40个数据分别落在4个组内,第一、二、四组的频数分别是5,12,8,则第三组的频数是________.
答案:
15
16. 若40个数据的平方和是56,平均数是$\frac{\sqrt{2}}{2}$,则这组数据的方差是________.
答案:
0.9
17. 已知一组数据的方差$s^{2}=\frac{1}{5}\times[(6 - 10)^{2}+(9 - 10)^{2}+(a - 10)^{2}+(11 - 10)^{2}+(b - 10)^{2}]=6.8$,则$a^{2}+b^{2}=$________.
答案:
296
18. 已知数据$x_{1},x_{2},\cdots,x_{n}$的平均数是5,方差是5,则数据$2x_{1}+3,2x_{2}+3,2x_{3}+3,\cdots,2x_{n}+3$的平均数是________,方差是________.
答案:
13 20 [解析]
∵数据x₁,x₂,⋯,xₙ的平均数是5,
∴数据2x₁ + 3,2x₂ + 3,2x₃ + 3,⋯,2xₙ + 3的平均数是2×5 + 3 = 13.
∵数据x₁,x₂,⋯,xₙ的方差是5,
∴数据2x₁ + 3,2x₂ + 3,2x₃ + 3,⋯,2xₙ + 3的方差是2²×5 = 20.
∵数据x₁,x₂,⋯,xₙ的平均数是5,
∴数据2x₁ + 3,2x₂ + 3,2x₃ + 3,⋯,2xₙ + 3的平均数是2×5 + 3 = 13.
∵数据x₁,x₂,⋯,xₙ的方差是5,
∴数据2x₁ + 3,2x₂ + 3,2x₃ + 3,⋯,2xₙ + 3的方差是2²×5 = 20.
19. (本题5分)某班在一次数学考试中,平均成绩是78分,男、女生的平均成绩分别是81分、75. 5分,求该班男、女生人数之比.
答案:
解:设男生人数为m人,女生人数为n人,
则有(m + n)×78 = m×81 + n×75.5,
即78m + 78n = 81m + 75.5n,
3m = 2.5n,m:n = 2.5:3 = 5:6.
∴男、女生人数之比为5:6.
则有(m + n)×78 = m×81 + n×75.5,
即78m + 78n = 81m + 75.5n,
3m = 2.5n,m:n = 2.5:3 = 5:6.
∴男、女生人数之比为5:6.
20. (本题6分)(衡阳中考)2025年3月31日是第30个全国中小学生安全教育日,为提高学生安全防范意识和自我防护能力,某学校举行了校园安全知识竞赛活动. 现从八、九年级中各随机抽取15名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,80分及以上为优秀,共分成四组,A:60≤x<70;B:70≤x<80;C:80≤x<90;D:90≤x≤100),并给出下面部分信息:
八年级抽取的学生竞赛成绩在C组中的数据为84,84,88.
九年级抽取的学生竞赛成绩为68,77,75,100,80,100,82,86,95,91,100,86,84,94,87.
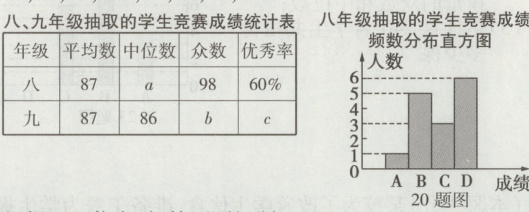
根据以上信息,解答下列问题:
(1)填空:a =________,b =________,c =________;
(2)该校八、九年级共500人参加了此次竞赛活动,请你估计该校八、九年级参加此次竞赛活动,成绩达到90分及以上的学生人数.
八年级抽取的学生竞赛成绩在C组中的数据为84,84,88.
九年级抽取的学生竞赛成绩为68,77,75,100,80,100,82,86,95,91,100,86,84,94,87.

根据以上信息,解答下列问题:
(1)填空:a =________,b =________,c =________;
(2)该校八、九年级共500人参加了此次竞赛活动,请你估计该校八、九年级参加此次竞赛活动,成绩达到90分及以上的学生人数.
答案:
解:
(1)84 100 80% [解析]八年级的竞赛成绩从小到大排列后,处在中间位置的数是84,因此中位数是84,即a = 84;九年级的竞赛成绩出现次数最多的是100,共出现3次,因此众数是100,即b = 100;九年级15名学生中竞赛成绩达到80分及以上的共有12人,因此优秀率为12/15×100% = 80%,即c = 80%.
故答案为84,100,80%.
(2)500×(6 + 6)/(15 + 15)= 200(人).
答:估计该校八、九年级参加此次竞赛活动,成绩达到90分及以上的学生人数为200人.
(1)84 100 80% [解析]八年级的竞赛成绩从小到大排列后,处在中间位置的数是84,因此中位数是84,即a = 84;九年级的竞赛成绩出现次数最多的是100,共出现3次,因此众数是100,即b = 100;九年级15名学生中竞赛成绩达到80分及以上的共有12人,因此优秀率为12/15×100% = 80%,即c = 80%.
故答案为84,100,80%.
(2)500×(6 + 6)/(15 + 15)= 200(人).
答:估计该校八、九年级参加此次竞赛活动,成绩达到90分及以上的学生人数为200人.
查看更多完整答案,请扫码查看


