2025年学考A加同步课时练九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学考A加同步课时练九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
6. 反比例函数$y = \frac{k}{x}(x < 0)$的图象如图所示,下列关于该函数图象的四个结论:①$k > 0$;②当$x < 0$时,$y$随$x$的增大而增大;

③该函数图象关于直线$y = -x$对称;④若点$(-2,3)$在该反比例函数图象上,则点$(-1,6)$也在该函数的图象上. 其中正确的结论有_________个.

③该函数图象关于直线$y = -x$对称;④若点$(-2,3)$在该反比例函数图象上,则点$(-1,6)$也在该函数的图象上. 其中正确的结论有_________个.
答案:
3【解析】观察反比例函数 $y=\frac{k}{x}(x < 0)$ 的图象可知图象在第二象限,
所以 $k < 0$,所以①错误;
因为当 $x < 0$时,$y$随 $x$ 的增大而增大,所以②正确;
因为该函数图象关于直线 $y=-x$对称,所以③正确;
因为点 $(-2,3)$在该反比例函数图象上,所以 $k=-6$,则点 $(-1,6)$也在该函数的图象上.所以④正确.
所以其中正确的结论有3个.
故答案为3.
所以 $k < 0$,所以①错误;
因为当 $x < 0$时,$y$随 $x$ 的增大而增大,所以②正确;
因为该函数图象关于直线 $y=-x$对称,所以③正确;
因为点 $(-2,3)$在该反比例函数图象上,所以 $k=-6$,则点 $(-1,6)$也在该函数的图象上.所以④正确.
所以其中正确的结论有3个.
故答案为3.
7. 若一个反比例函数的图象经过点$A(m,m)$和$B(2m,-1)$,则这个反比例函数的解析式为______________.
答案:
$y=\frac{4}{x}$【解析】设反比例函数的解析式为 $y=\frac{k}{x}(k\neq0)$,
$\because$反比例函数的图象经过点 $A(m,m)$ 和 $B(2m,-1)$, $\therefore k=m^{2}=-2m$,
解得 $m_1=-2,m_2=0$(舍去), $\therefore k=4$.
$\therefore$反比例函数的解析式为 $y=\frac{4}{x}$.
故答案为: $y=\frac{4}{x}$.
$\because$反比例函数的图象经过点 $A(m,m)$ 和 $B(2m,-1)$, $\therefore k=m^{2}=-2m$,
解得 $m_1=-2,m_2=0$(舍去), $\therefore k=4$.
$\therefore$反比例函数的解析式为 $y=\frac{4}{x}$.
故答案为: $y=\frac{4}{x}$.
8. 如图,在平面直角坐标系中,正方形$ABCD$的顶点$A$与$D$在函数$y = \frac{k}{x}(x > 0)$的图象上,$AC \perp x$轴,垂足为$C$,点$B$的坐标为$(0,2)$,

则$k$的值为_________.

则$k$的值为_________.
答案:
8【解析】如图,连接BD,与AC交于点$O'$, $\because$四边形ABCD是正方形,$AC⊥ x$轴,
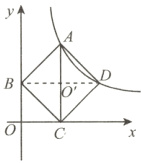
$\therefore BD$平行于 $x$轴.
$\because B(0,2),\therefore O'C=BO'=AO'=DO'=2$
$\therefore$点 $A$的坐标为$(2,4)$,
$\therefore k=2\times4 = 8$
故答案为:8.
8【解析】如图,连接BD,与AC交于点$O'$, $\because$四边形ABCD是正方形,$AC⊥ x$轴,

$\therefore BD$平行于 $x$轴.
$\because B(0,2),\therefore O'C=BO'=AO'=DO'=2$
$\therefore$点 $A$的坐标为$(2,4)$,
$\therefore k=2\times4 = 8$
故答案为:8.
9. 如图,已知菱形$ABCD$的对称中心是坐标原点$O$,四个顶点都在坐标轴上,反比例函数$y = \frac{k}{x}(k \neq 0)$的图象与$AD$边交于$E(-4,\frac{1}{2})$,$F(m,2)$两点.
(1)求$k$,$m$的值;
(2)写出函数$y = \frac{k}{x}$图象在菱形$ABCD$内$x$的取值范围.

(1)求$k$,$m$的值;
(2)写出函数$y = \frac{k}{x}$图象在菱形$ABCD$内$x$的取值范围.

答案:
解:
(1) $\because$点 $E(-4,\frac{1}{2})$在 $y=\frac{k}{x}$ 的图象上,
$\therefore k=-2$
$\therefore$反比例函数的解析式为 $y=-\frac{2}{x}$
$\because$点 $F(m,2)$在 $y=-\frac{2}{x}$ 的图象上
$\therefore m=-1$
(2) 函数 $y=\frac{k}{x}$图象在菱形 $ABCD$内 $x$ 的取值范围为: $-4 < x < -1$或 $1 < x < 4$.
(1) $\because$点 $E(-4,\frac{1}{2})$在 $y=\frac{k}{x}$ 的图象上,
$\therefore k=-2$
$\therefore$反比例函数的解析式为 $y=-\frac{2}{x}$
$\because$点 $F(m,2)$在 $y=-\frac{2}{x}$ 的图象上
$\therefore m=-1$
(2) 函数 $y=\frac{k}{x}$图象在菱形 $ABCD$内 $x$ 的取值范围为: $-4 < x < -1$或 $1 < x < 4$.
10. 如图,在平面直角坐标系中,矩形$ABCD$的边$AB$在$x$轴正半轴上(点$B$在点$A$的右侧),$AB = 3$,$AD = 8$,$AD \perp x$轴,$CD$在第一象限,边$AD$的中点$E$在函数$y = \frac{k}{x}(x > 0)$的图象上,边$BC$交该函数图象于点$F$,连接$BE$.
(1)求$BE$的长;
(2)若$CF - BE = 2$,求$k$的值.

(1)求$BE$的长;
(2)若$CF - BE = 2$,求$k$的值.

答案:
解:
(1)由题意可知 $AE = 4$
$\because$矩形 $ABCD$的边 $AB$在 $x$轴正半轴上,$AD⊥ x$轴,且 $AB = 3$
$\therefore BE=\sqrt{AB^{2}+AE^{2}}=\sqrt{3^{2}+4^{2}} = 5$
(2) $\because BE = 5,CF - BE = 2$
$\therefore CF = 7$
$\because BC = AD = 8$
$\therefore BF = 8 - 7 = 1$
设 $E(m,4)$则 $F(m + 3,1)$
$\because$点 $E,F$ 在函数 $y=\frac{k}{x}(x>0)$ 的图象上
$\therefore k = 4m=(m + 3)\times1$
解得 $m = 1$
$\therefore k = 4$
(1)由题意可知 $AE = 4$
$\because$矩形 $ABCD$的边 $AB$在 $x$轴正半轴上,$AD⊥ x$轴,且 $AB = 3$
$\therefore BE=\sqrt{AB^{2}+AE^{2}}=\sqrt{3^{2}+4^{2}} = 5$
(2) $\because BE = 5,CF - BE = 2$
$\therefore CF = 7$
$\because BC = AD = 8$
$\therefore BF = 8 - 7 = 1$
设 $E(m,4)$则 $F(m + 3,1)$
$\because$点 $E,F$ 在函数 $y=\frac{k}{x}(x>0)$ 的图象上
$\therefore k = 4m=(m + 3)\times1$
解得 $m = 1$
$\therefore k = 4$
查看更多完整答案,请扫码查看


