《2025年学考A加同步课时练九年级数学下册人教版》

1. 斜面坡度是指坡面的_______与_______的比.

答案： 铅直高度，水平宽度

2. 利用解直角三角形的知识解决实际问题的一般步骤：
(1) 将实际问题抽象成_______；(2) 根据条件，适当选用_______等解直角三角形；(3) 得到数学问题答案；(4) 得到实际问题答案.

答案：
(1)数学问题;
(2)锐角三角函数

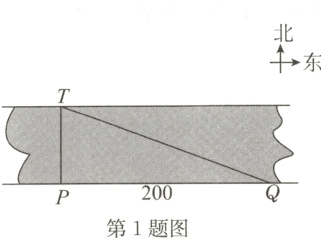
1. 如图，为了测量一条河流的宽度，一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置，T在P的正北方向，且T在Q的北偏西70°方向，则河宽(PT的长)可以表示为（ ）

A. 200tan70°米
B. $\frac{200}{tan70^{\circ}}$米
C. 200sin70°米
D. $\frac{200}{sin70^{\circ}}$米

答案： B [解析]在Rt△PQT中，
∵∠QPT = 90°，∠PQT = 90° - 70° = 20°，
∴∠PTQ = 70°，
∴tan70° = $\frac{PQ}{PT}$，
∴PT = $\frac{PQ}{tan70°}$ = $\frac{200}{tan70°}$，即河宽为$\frac{200}{tan70°}$米，故选B。

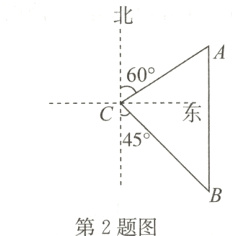
2. 如图，一艘轮船从位于灯塔C的北偏东60°方向，距离灯塔60 n mile的小岛A出发，沿正南方向航行一段时间后，到达位于灯塔C的南偏东45°方向上的B处，这时轮船B与小岛A的距离是（ ）

A. 30$\sqrt{3}$ n mile
B. 60 n mile
C. 120 n mile
D. （30＋30$\sqrt{3}$）n mile

答案：
D [解析]如图，过C作CD⊥AB于D点，
∴∠ACD = 30°，∠BCD = 45°，AC = 60。 在Rt△ACD中，cos∠ACD = $\frac{CD}{AC}$，sin∠ACD = $\frac{AD}{AC}$，
∴CD = AC·cos∠ACD = 60×$\frac{\sqrt{3}}{2}$ = 30$\sqrt{3}$，AD = AC·sin∠ACD = 30。在Rt△DCB中，
∵∠BCD = ∠B = 45°，
∴CD = BD = 30$\sqrt{3}$
∴AB = AD + BD = 30 + 30$\sqrt{3}$故选D。

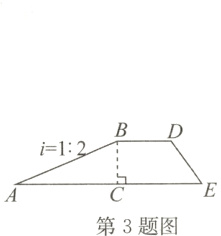
3. 如图，大坝横截面的迎水坡AB的坡比为1∶2，即BC∶AC = 1∶2，若坡面AB的水平宽度AC为12米，则斜坡AB的长为（ ）

A. 4$\sqrt{3}$米
B. 6$\sqrt{3}$米
C. 6$\sqrt{5}$米
D. 24米

答案： C[解析]
∵大坝横截面的迎水坡AB的坡比为1:2，AC = 12米，
∴$\frac{BC}{AC}$ = $\frac{1}{2}$ = $\frac{BC}{12}$，
∴BC = 6，
∴AB = $\sqrt{AC^{2}+BC^{2}}$ = $\sqrt{12^{2}+6^{2}}$ = 6$\sqrt{5}$(米)。故选C。

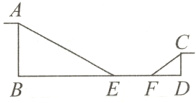
4. 为满足广大滑板爱好者的需求，某广场修建了一个小型滑板场，如图，爱好者们从A处滑下，经缓冲区EF之后，滑向C处，已知AB⊥BD于点B，CD⊥BD于点D，AB = 2CD，BD = 13 m，缓冲区EF = 3 m，斜坡轨道AE的坡度（或坡比）i = 1∶2，斜坡轨道FC的坡角为37°，其中B、E、F、D在同一直线上，则AB的长度为（参考数据：tan37°≈0.75，sin37°≈0.60，cos37°≈0.80）（ ）

A. 3.55 m
B. 3.75 m
C. 3.95 m
D. 4.15 m

答案： B[解析]
∵AB = 2CD，
∴设DC = x，则AB = 2x。
∵tan37°≈0.75，
∴$\frac{CD}{DF}$ = $\frac{x}{DF}$ = 0.75，则DF = $\frac{4}{3}$x，
∵斜坡轨道AE的坡度(或坡比)i = 1:2，
∴BE = 2AB = 4x，故BD - EF = BE + FD = 13 - 3 = 4x + $\frac{4}{3}$x，解得x = $\frac{15}{8}$，故AB = 2×$\frac{15}{8}$ = $\frac{15}{4}$ = 3.75(m)。故选B。