2025年学考A加同步课时练九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学考A加同步课时练九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
5.如图,在△ABC中,∠BAC = 120°,AC = 6,AB = 4,求BC的长。


答案:
解:如图,过点C作CD⊥AB,交BA的延长线于点D,
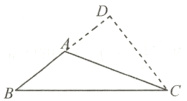
∵∠BAC = 120°,
∴∠DAC = 180° - 120° = 60°,
∴∠ACD = 30°,
∴ $AD=\frac{1}{2}AC = 3$,
∴BD = AB + AD = 7,
由勾股定理得, $CD=\sqrt{AC^{2}-AD^{2}}=3\sqrt{3}$
在Rt△BCD中, $BC=\sqrt{BD^{2}+CD^{2}}=2\sqrt{19}$
解:如图,过点C作CD⊥AB,交BA的延长线于点D,

∵∠BAC = 120°,
∴∠DAC = 180° - 120° = 60°,
∴∠ACD = 30°,
∴ $AD=\frac{1}{2}AC = 3$,
∴BD = AB + AD = 7,
由勾股定理得, $CD=\sqrt{AC^{2}-AD^{2}}=3\sqrt{3}$
在Rt△BCD中, $BC=\sqrt{BD^{2}+CD^{2}}=2\sqrt{19}$
6.如图,在Rt△ABC中,∠C = 90°,AB的垂直平分线与AB,BC分别交于点E和点D,且BD = 2AC。
(1)求∠B的度数;
(2)求tan∠BAC(结果保留根号)。

(1)求∠B的度数;
(2)求tan∠BAC(结果保留根号)。

答案:
解:
(1)如图,连接AD。
∵DE垂直平分线段AB,
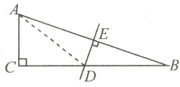
∴DA = DB,
∴∠B = ∠DAB。
∵BD = 2AC,
∴AD = 2AC。
∵∠C = 90°,
∴∠ADC = 30°。
∵∠ADC = ∠DAB + ∠B,
∴∠B = 15°。
(2)设AC = a,则AD = BD = 2a, $CD=\sqrt{3}a$,
BC = $2a + \sqrt{3}a$,
∴ $\tan\angle BAC=\frac{BC}{AC}=\frac{2a + \sqrt{3}a}{a}=2 + \sqrt{3}$;
解:
(1)如图,连接AD。
∵DE垂直平分线段AB,

∴DA = DB,
∴∠B = ∠DAB。
∵BD = 2AC,
∴AD = 2AC。
∵∠C = 90°,
∴∠ADC = 30°。
∵∠ADC = ∠DAB + ∠B,
∴∠B = 15°。
(2)设AC = a,则AD = BD = 2a, $CD=\sqrt{3}a$,
BC = $2a + \sqrt{3}a$,
∴ $\tan\angle BAC=\frac{BC}{AC}=\frac{2a + \sqrt{3}a}{a}=2 + \sqrt{3}$;
7.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD,若AC = 2,求tanD。


答案:
解:如图,连接BC,
∵AB是⊙O的直径,
∴∠ACB = 90°。
∵AB = 6,AC = 2,
∴ $BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{6^{2}-2^{2}}=4\sqrt{2}$
又
∵∠D = ∠A,
∴ $\tan D=\tan A=\frac{BC}{AC}=\frac{4\sqrt{2}}{2}=2\sqrt{2}$

解:如图,连接BC,
∵AB是⊙O的直径,
∴∠ACB = 90°。
∵AB = 6,AC = 2,
∴ $BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{6^{2}-2^{2}}=4\sqrt{2}$
又
∵∠D = ∠A,
∴ $\tan D=\tan A=\frac{BC}{AC}=\frac{4\sqrt{2}}{2}=2\sqrt{2}$

8.如图,在边长相同的小正方形网格中,点A,B,C,D,E都在这些小正方形的顶点上,AB,CD相交于点P,求AP/PB和tan∠APD的值。


答案:
解:
∵四边形BCED是正方形,
∴DB//AC,△CAP∽△DBP,
∴ $\frac{AP}{PB}=\frac{AC}{DB}=3$。
如图,连接BE,
∵四边形BCED是正方形,
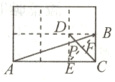
∴ $DF = CF=\frac{1}{2}CD$,
$BF=\frac{1}{2}BE$,CD = BE,BE⊥CD,BF = CF,
∵△ACP∽△DBP,
∴DP:CP = BD:AC = 1:3,
∴DP:DF = 1:2,
∴ $DP = PF=\frac{1}{2}CF=\frac{1}{2}BF$,
在Rt△PBF中, $\tan\angle BPF=\frac{BF}{PF}=2$,
∵∠APD = ∠BPF,
∴ $\tan\angle APD = 2$。
解:
∵四边形BCED是正方形,
∴DB//AC,△CAP∽△DBP,
∴ $\frac{AP}{PB}=\frac{AC}{DB}=3$。
如图,连接BE,
∵四边形BCED是正方形,

∴ $DF = CF=\frac{1}{2}CD$,
$BF=\frac{1}{2}BE$,CD = BE,BE⊥CD,BF = CF,
∵△ACP∽△DBP,
∴DP:CP = BD:AC = 1:3,
∴DP:DF = 1:2,
∴ $DP = PF=\frac{1}{2}CF=\frac{1}{2}BF$,
在Rt△PBF中, $\tan\angle BPF=\frac{BF}{PF}=2$,
∵∠APD = ∠BPF,
∴ $\tan\angle APD = 2$。
查看更多完整答案,请扫码查看


