《2025年学考A加同步课时练九年级数学下册人教版》

1. 由直角三角形中的已知元素，求出其余________的过程，叫做解直角三角形.

答案： 未知元素

2. 直角三角形中，除直角外，其余五个元素之间有如下关系:　
(1) 三边之间的关系：$a^{2}+b^{2}=$________（勾股定理）.
(2) 两锐角之间的关系：$\angle A + \angle B =$________.
(3) 边角之间的关系：三角函数（________、________、________）.

答案： $c^{2}$
@@$90^{\circ}$
@@正弦、余弦、正切

1. 在$\triangle ABC$中，$\angle A = 40^{\circ}$，$\angle C = 90^{\circ}$，$BC = 7$，则$AB$边的长是（ ）
A. $7\sin40^{\circ}$
B. $7\cos40^{\circ}$
C. $\frac{7}{\sin40^{\circ}}$
D. $\frac{7}{\cos40^{\circ}}$

答案： C　[解析]
∵在△ABC中,∠A = 40°,∠C = 90°,BC = 7,
∴sinA = $\frac{BC}{AB}$,
∴AB = $\frac{BC}{sinA}=\frac{7}{sin40^{\circ}}$.故选C.

2. 某简易房的示意图如图所示，它是一个轴对称图形，则坡屋顶上弦杆$AC$的长为（ ）
A. $\frac{5}{11\sin\alpha}$米 B. $\frac{5}{11\cos\alpha}$米 C. $\frac{11}{5\sin\alpha}$米 D. $\frac{11}{5\cos\alpha}$米
　　　　　　　　　　　　　　　　　　　　　　

答案：
D　[解析]如图，过点A作AH⊥BC于H.
　　　　　
由题意得AB = AC,BC = 4 + 0.2 + 0.2 = 4.4(米),
∵AH⊥BC,
∴BH = CH = 2.2(米),
∴AC = AB = $\frac{BH}{cos\alpha}=\frac{2.2}{cos\alpha}=\frac{11}{5cos\alpha}$(米)，故选D.

3. 在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$\cos A = \frac{\sqrt{3}}{2}$，$\angle B$的平分线$BD$交$AC$于点$D$，若$AD = 16$，则$BC$长为（ ）
A. 6
B. 8
C. $8\sqrt{3}$
D. 12

答案：
C　[解析]如图
　　　　　　　　　　　　
∵cosA = $\frac{\sqrt{3}}{2}$，
∴∠A = 30°.
∵∠C = 90°,
∴∠ABC = 60°.
∵BD平分∠ABC,
∴∠ABD = ∠A = ∠CBD = 30°,
∴DB = DA = 16,
∴BC = BD·cos30° = 16×$\frac{\sqrt{3}}{2}=8\sqrt{3}$,故选C.

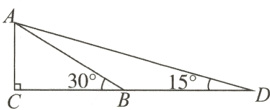
4. 构建几何图形解决代数问题是“数形结合”思想的重要性，在计算$\tan15^{\circ}$时，如图，在$Rt\triangle ACB$中， $\angle C = 90^{\circ}$，$\angle ABC = 30^{\circ}$，延长$CB$使$BD = AB$，连接$AD$，得$\angle D = 15^{\circ}$，所以$\tan15^{\circ}=\frac{AC}{CD}=\frac{1}{2 + \sqrt{3}}=\frac{2 - \sqrt{3}}{(2 + \sqrt{3})(2 - \sqrt{3})}=2 - \sqrt{3}$. 类比这种方法，计算$\tan22.5^{\circ}$的值为（ ）


A. $\sqrt{2}+1$
B. $\sqrt{2}-1$
C. $\sqrt{2}$
D. $\frac{1}{2}$

答案：
B　[解析]如图,在Rt△ACB中,∠C = 90°,∠ABC = 45°,延长CB使BD = AB,连接AD,得∠D = 22.5°.设AC = BC = 1，则AB = BD = $\sqrt{2}$,
　　　　　　　　　　　　
∴tan22.5° = $\frac{AC}{CD}=\frac{1}{1 + \sqrt{2}}=\sqrt{2}-1$,故选B.