《2025年学考A加同步课时练九年级数学下册人教版》

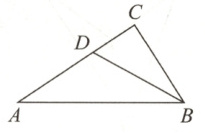
8. 如图，在Rt△ABC中，∠C=90°，D为AC上的一点，CD=3，AD=BD=5。求∠A的三个三角函数值。

答案： 解:在Rt△BCD中,
∵CD = 3,BD = 5,
∴BC = $\sqrt{BD^{2}-CD^{2}}=\sqrt{5^{2}-3^{2}}$ = 4,又AC = AD + CD = 8,
∴AB = $\sqrt{AC^{2}+BC^{2}}=\sqrt{8^{2}+4^{2}}$ = 4$\sqrt{5}$,则sinA = $\frac{BC}{AB}=\frac{4}{4\sqrt{5}}=\frac{\sqrt{5}}{5}$,cosA = $\frac{AC}{AB}=\frac{8}{4\sqrt{5}}=\frac{2\sqrt{5}}{5}$,tanA = $\frac{BC}{AC}=\frac{4}{8}=\frac{1}{2}$.

9. 如图，在锐角三角形ABC中，AB=10，BC=9，△ABC的面积为27。求tanB的值。

答案：
解:如图,过点A作AH⊥BC于H,
∵$S_{\triangle ABC}$ = 27,
∴$\frac{1}{2}$×9×AH = 27,
∴AH = 6,
∵AB = 10,
∴BH = $\sqrt{AB^{2}-AH^{2}}=\sqrt{10^{2}-6^{2}}$ = 8,
∴tanB = $\frac{AH}{BH}=\frac{6}{8}=\frac{3}{4}$.

10. 在Rt△ABC中，∠C=90°，sinA=$\frac{5}{13}$，求sinB的值。

答案： 解:
∵Rt△ABC中,∠C = 90°,sinA = $\frac{5}{13}$,
∴cosA = $\sqrt{1 - sin^{2}A}=\sqrt{1 - (\frac{5}{13})^{2}}=\frac{12}{13}$,
∵∠A + ∠B = 90°,
∴sinB = cosA = $\frac{12}{13}$.