2025年学考A加同步课时练九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学考A加同步课时练九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么
位似图形对应点的坐标的比等于____________.即原图形上的点的坐标为(x,y),对应]的位似图形上的点的坐标为____________或____________
答案:
k或-k (kx,ky),(-kx,-ky)
1.如图,在平面直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点
O为位似中心,在第三象限内作与△OAB的位似比为$\frac{1}{3}$的位似图形△OCD,
则点C的坐标为 ( )
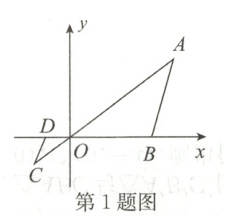
A.(−1,−1)
B.( −$\frac{4}{3}$,−1)
C.(−1,− $\frac{4}{3}$)
D.(−2,−1)
O为位似中心,在第三象限内作与△OAB的位似比为$\frac{1}{3}$的位似图形△OCD,
则点C的坐标为 ( )

A.(−1,−1)
B.( −$\frac{4}{3}$,−1)
C.(−1,− $\frac{4}{3}$)
D.(−2,−1)
答案:
B[解析]
∵以点O为位似中心,位似比为$\frac{1}{3}$,而A(4,3),
∴A点的对应点C的坐标为$(-\frac{4}{3},-1)$.故选B.
∵以点O为位似中心,位似比为$\frac{1}{3}$,而A(4,3),
∴A点的对应点C的坐标为$(-\frac{4}{3},-1)$.故选B.
2.如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),
C(3,1),以原点为位似中心,在原点的右侧画△DEF,使△DEF与△ABC成
位似图形,且相似比为2:1,则线段DF的长度为 ( )
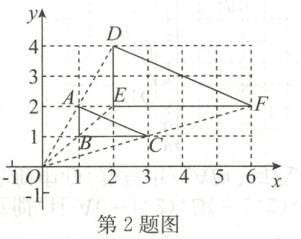
A.$\sqrt{5}$
B.2
C.4
D.2$\sqrt{5}$
C(3,1),以原点为位似中心,在原点的右侧画△DEF,使△DEF与△ABC成
位似图形,且相似比为2:1,则线段DF的长度为 ( )

A.$\sqrt{5}$
B.2
C.4
D.2$\sqrt{5}$
答案:
D[解析]
∵以原点为位似中心,在原点的右侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,而A(1,2),C(3,1),
∴D(2,4),F(6,2),
∴$DF=\sqrt{(2 - 6)^{2}+(4 - 2)^{2}}=2\sqrt{5}$.故选D.
∵以原点为位似中心,在原点的右侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,而A(1,2),C(3,1),
∴D(2,4),F(6,2),
∴$DF=\sqrt{(2 - 6)^{2}+(4 - 2)^{2}}=2\sqrt{5}$.故选D.
3.如图,两个三角形是以点P为位似中心的位似图形,则点P的坐标是( )
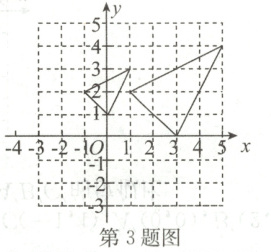
A.(−3,2)
B.(−3,1)
C.(2,−3)
D.(−2,3)

A.(−3,2)
B.(−3,1)
C.(2,−3)
D.(−2,3)
答案:
A[解析]如图,点P为位似中心,
∴点P的坐标为(-3,2),故选A
A[解析]如图,点P为位似中心,
∴点P的坐标为(-3,2),故选A

4.如图,在平面直角坐标系中,已知点A(−3,−1),B(0,−2),P(1,1),以点P为
位似中心,把△PAB放大为原来的2倍,得到△PA'B',则A'的坐标为 ( )
A.(6,2) B.(6,5) C.(9,3) D.(9,5)

位似中心,把△PAB放大为原来的2倍,得到△PA'B',则A'的坐标为 ( )
A.(6,2) B.(6,5) C.(9,3) D.(9,5)

答案:
D[解析]如图所示,过点A'作A'D⊥x轴于点D,过点A作AE⊥x轴于点E,过点P作x轴的平行线,交A'D于点F,交AE延长线于点C,由题意可得△ACP∽△A'FP,
∵A(-3,-1),P(1,1)
∴CP=3 + 1=4,AC=1 + 1=2.
∵以点P为位似中心,把△PAB放大为原来的2倍,
∴$\frac{CP}{PF}=\frac{AC}{A'F}=\frac{1}{2}$,
∴PF=8,A'F=4,
∴A'D=5,
∴A'的坐标为(9,5).故选D.
D[解析]如图所示,过点A'作A'D⊥x轴于点D,过点A作AE⊥x轴于点E,过点P作x轴的平行线,交A'D于点F,交AE延长线于点C,由题意可得△ACP∽△A'FP,
∵A(-3,-1),P(1,1)
∴CP=3 + 1=4,AC=1 + 1=2.
∵以点P为位似中心,把△PAB放大为原来的2倍,
∴$\frac{CP}{PF}=\frac{AC}{A'F}=\frac{1}{2}$,
∴PF=8,A'F=4,
∴A'D=5,
∴A'的坐标为(9,5).故选D.

5.如图,△AOB三个顶点的坐标分别为A(5,0),O(0,0),B(3,6),以点O为位似
中心,相似比为$\frac{2}{3}$,将△AOB缩小,则点B的对应点B'的坐标是____________.
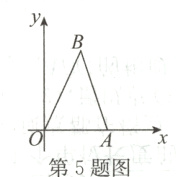
中心,相似比为$\frac{2}{3}$,将△AOB缩小,则点B的对应点B'的坐标是____________.

答案:
(2,4)或(-2,-4)[解析]如图,
∵△OAB∽△OA'B',相似比为$\frac{3}{2}$,B(3,6),
∴B'(2,4).根据对称性可知,△OA''B''在第三象限时,B''(-2,-4),
∴满足条件的点B'的坐标为(2,4)或(-2,-4).故答案为(2,4)或(-2,-4).
(2,4)或(-2,-4)[解析]如图,
∵△OAB∽△OA'B',相似比为$\frac{3}{2}$,B(3,6),
∴B'(2,4).根据对称性可知,△OA''B''在第三象限时,B''(-2,-4),
∴满足条件的点B'的坐标为(2,4)或(-2,-4).故答案为(2,4)或(-2,-4).

查看更多完整答案,请扫码查看


