2025年学考A加同步课时练九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学考A加同步课时练九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 对于两个多边形,如果它们的对应顶点的连线相交于________,并且这点与对应顶点所连线段________,那么这两个多边形叫做位似多边形,这个点叫做________.
答案:
一点,成比例,位似中心.
2. 位似图形是________图形,对应边互相________.
答案:
相似,平行.
1. 下列图形中不是位似图形的为 ( )


答案:
B【解析】对应顶点的连线相交于一点的两个相似多边形叫位似图形.
根据位似图形的概念,A、C、D三个图形中的两个图形都是位似图形;
B中的两个图形不符合位似图形的概念,对应边不平行,故不是位似图形.
故选B.
根据位似图形的概念,A、C、D三个图形中的两个图形都是位似图形;
B中的两个图形不符合位似图形的概念,对应边不平行,故不是位似图形.
故选B.
2. 下列说法中,正确的个数是 ( )
①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A'B'C'D'E'位似,则其中△ABC与△A'B'C'也位似,且位似比相等.
A. 1 B. 2 C. 3 D. 4
①位似图形一定是相似图形;②相似图形一定是位似图形;③两个位似图形若全等,则位似中心在两个图形之间;④若五边形ABCDE与五边形A'B'C'D'E'位似,则其中△ABC与△A'B'C'也位似,且位似比相等.
A. 1 B. 2 C. 3 D. 4
答案:
C【解析】位似图形一定是相似图形,①说法正确;
相似图形不一定是位似图形,②说法错误;
两个位似图形若全等,则位似中心在两个图形之间,③说法正确;
若五边形ABCDE与五边形A'B'C'D'E'位似,则其中△ABC与△A'B'C'也位似,且位似比相等,④说法正确.
故选C.
相似图形不一定是位似图形,②说法错误;
两个位似图形若全等,则位似中心在两个图形之间,③说法正确;
若五边形ABCDE与五边形A'B'C'D'E'位似,则其中△ABC与△A'B'C'也位似,且位似比相等,④说法正确.
故选C.
3. 如图所示,两个三角形是位似图形,它们的位似中心是 ( )
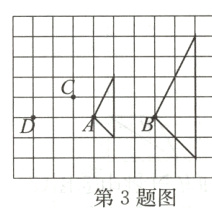
A. 点A
B. 点B
C. 点C
D. 点D

A. 点A
B. 点B
C. 点C
D. 点D
答案:
D【解析】如图,
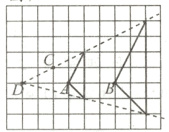
两个三角形是位似图形,它们的位似中心是点D.
故选D.
D【解析】如图,

两个三角形是位似图形,它们的位似中心是点D.
故选D.
4. 如图,△ABC与△DEF位似,点O为位似中心. 已知OA:OD = 1:2,则△ABC与△DEF的面积比为 ( )
A. 1:2 B. 1:3 C. 1:4 D. 1:5
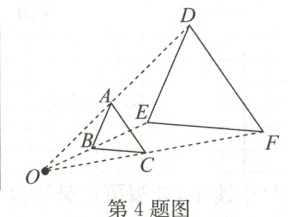
A. 1:2 B. 1:3 C. 1:4 D. 1:5

答案:
C【解析】
∵△ABC与△DEF是位似图形,OA:OD = 1:2,
∴△ABC与△DEF的位似比是1:2.
∴△ABC与△DEF的相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
故选C.
∵△ABC与△DEF是位似图形,OA:OD = 1:2,
∴△ABC与△DEF的位似比是1:2.
∴△ABC与△DEF的相似比为1:2,
∴△ABC与△DEF的面积比为1:4,
故选C.
5. 如图,已知△ABC与△DEF位似,位似中心为O,且△ABC的面积与△DEF的面积之比是16:9,则$\frac{AO}{AD}$=________.


答案:
$\frac{4}{7}$【解析】
∵△ABC与△DEF位似,
∴AB//DE,△ABC∽△DEF.
∵△ABC的面积与△DEF的面积之比是16:9,
∴△ABC与△DEF的相似比是4:3,即$\frac{AB}{DE}=\frac{4}{3}$.
∵AB//DE,
∴△OAB∽△ODE,
∴$\frac{OA}{OD}=\frac{AB}{DE}=\frac{4}{3}$,
∴$\frac{AO}{AD}=\frac{4}{7}$.
∵△ABC与△DEF位似,
∴AB//DE,△ABC∽△DEF.
∵△ABC的面积与△DEF的面积之比是16:9,
∴△ABC与△DEF的相似比是4:3,即$\frac{AB}{DE}=\frac{4}{3}$.
∵AB//DE,
∴△OAB∽△ODE,
∴$\frac{OA}{OD}=\frac{AB}{DE}=\frac{4}{3}$,
∴$\frac{AO}{AD}=\frac{4}{7}$.
查看更多完整答案,请扫码查看


